2019 Spotlight
Beginning in the earliest grades, DRK-12 projects are promoting access to and success in Algebra for all students, through pre-service training and professional learning opportunities for teachers, instructional materials, assessments, learning technologies, interventions for at-risk students, and other innovations.
In this Spotlight...
- Community Voice by Colleen Henry
- Featured DRK-12 Projects
- Advancing Reasoning (PI: Kevin Moore)
- The Algebra Project Mathematics Content and Pedagogy Initiative (APMCPI) (PI: Oliver Hill)
- Algebraic Knowledge for Teaching: A Cross-cultural Perspective (PI: Meixia Ding)
- Algebraic Learning and Cognition in Learning Disabled Students (PI: David Geary)
- Assessing Secondary Teachers' Algebraic Habits of Mind (PIs: Matsuura, Stevens, Sword)
- Developing Preservice Teachers' Capacity to Teach Students with Learning Disabilities in Algebra I (PI: Casey Hord)
- Development and Empirical Recovery for a Learning Progression-Based Assessment of the Function Concept (PI: Edith Aurora Graf)
- Flipped Math Study (PI: Zandra de Araujo)
- Investigating Differentiated Instruction and Relationships between Rational Number Knowledge and Algebraic Reasoning in Middle School (IDReAM) (PI: Amy Hackenberg)
- LEAP V: Identifying Effective Instructional Practices that Foster the Development of Algebraic Thinking in Elementary School (PI: Eric Knuth)
- Measuring Early Mathematical Reasoning Skills: Developing Tests of Numerical Relational and Spatial Reasoning (PI: Leanne Ketterlin Geller)
- Project LEAP: Learning through an Early Algebra Progression (Suite of NSF-Funded Projects, Including NSF #1720129 - PI: Maria Blanton)
- Teaching and Learning Algebraic Thinking with PhET Interactive Simulations (PI: Katherine Perkins)
- Using Math Pathways & Pitfalls to Promote Algebra Readiness (PI: Jodi Davenport)
- Video in the Middle: Flexible Digital Experiences for Mathematics Teacher Education (PI: Nanette Seago)
See the 2024 Spotlight on Algebra Education in DRK-12.
Algebra in the Early Grades: Setting the Stage for Future Studies and a Math Mindset
Colleen Henry, Fairview Elementary School, Auburn, ME

The early elementary years are critical in setting the stage for a love of math. Young children are naturally curious and eager to learn new ideas. I believe that it is at this age that children can learn to be flexible problem solvers and develop a growth mindset about themselves as learners, which is especially important if our goal is to build future classrooms of higher level mathematicians.
In my math workshop, we work on being flexible problem solvers in a number of ways. Students solve Open Task problems on a regular basis in math workshop. Open tasks allow students to attack the problem at their own entry point, feel successful, and witness how many different solutions there can be to the same problem. Implementing open task problems has been a huge shift. In the past, students would work on solving word problems that had one and only one correct answer. Quick problem solvers were done right away and the mathematical thinking ended right there. Students that were slower to process the problem often gave up and began to feel negatively about themselves as math students. By using open tasks, my students have realized that problem solving doesn’t end with one answer, they continue finding other solutions that could work to solve their problems and are extremely motivated to do so! Students are able to have powerful dialogue about their solutions because of the variety of solutions that occur from open tasks. Hearing second graders ask each other why they selected various strategies and models is not something I would have expected for such young children, but it happens daily now! Seeing students not want math time to end has been amazing to witness and very validating.
Using a variety of tools to make visual representations of their thinking is another way we are preparing our young mathematicians. Students are learning to explain their thinking and work through their problem solving with tools such as open number lines, base-ten blocks, and ten frames. The use of manipulatives and visuals has really helped to raise the level of dialogue and understanding of many math concepts for the students. Students are able to model their thinking using a variety of tools and act as math mentors to their peers. In the past, the struggling math students used manipulatives, and there was a mindset by the students that only struggling math students should use them. By expecting all students to model their thinking with a visual tool and to explain their thinking, all students have raised their math skills and added to their bag of tricks for solving problems.
I believe that the early elementary years set the stage for a math mindset. We often hear of math anxiety or people labeling themselves as “not a math person”. My hope is that with more classrooms having the opportunity to learn about open taks, visual representations to aid in explaining their thinking, and creating opportunities for dialogue in problem solving, we will have far less math anxiety are much more flexible problem solvers confident in their understanding and ability to work through challenges. Professional development for early elementary educators is critical for this to happen.
Featured Projects
 Advancing Reasoning (NSF #1350342)
Advancing Reasoning (NSF #1350342)
PI: Kevin Moore
Grades: 6-14
Specific Content/Skills/Types of Reasoning Addressed: We address quantitative and covariational reasoning in the context of graphing, function, algebra, and modeling.
Intervention or Approach: We seek to support students’ and pre-/in-service teachers' mathematical thinking and learning. We eschew traditional topical approaches to teaching mathematics, and instead work to create experiences that capture our evolving understandings of how students think and learn. We work closely with students through an iterative, cognitive-based approach to develop and test models of student thinking and learning. We also work closely with teachers to support their modifying and implementing curricula in ways that give their students mathematical autonomy in the classroom. This approach allows us to develop products that create transformative learning experiences by tapping the creativity of students and teachers.
Key Challenge: A key challenge in our work is trying to put ourselves in the shoes of our students. Because of the fundamental impossibility of knowing how another person is thinking, we have to work in strategic ways to construct, test, and refine models of student thinking. To address this constraint, we strategically use both conventional and unconventional mathematical representations in our work. When only using conventional representations, it is difficult to determine if a student has constructed a concept. By using unconventional representations, we are able to determine if a student has constructed a concept that lets them see those representations as conveying the same mathematical ideas as more conventional representations. In short, we define a concept as a meaning that enables the learner to see situations that are perceptually different as mathematically equivalent.
Theoretical Framework: We draw on von Glasersfeld’s Radical Constructivism, which has its roots in Piaget’s Genetic Epistemology. Similarly, we draw on notions of quantitative and covariational reasoning put forth by mathematics educators including Marilyn Carlson, Patrick Thompson, and Leslie Steffe.
Methodology: Our primary methodological approach relies on a combination of teaching experiments, exploratory teaching, and semi-structured clinical interviews. We use these methodologies to construct, test, and refine tentative models of student thinking. Consistent with our theoretical framework, these models are not considered one-to-one matches with students’ actual mathematical realities, but rather models that provide viable explanations for students’ actions and behaviors.
Products: Teaching Activities | Interview Tasks | Publications | Presentations
The Algebra Project Mathematics Content and Pedagogy Initiative (APMCPI) (NSF #1749483)
PI: Oliver Hill
Grades: 6-12
Specific Content/Skills/Types of Reasoning Addressed: To prepare mathematics teachers on the AP cooperative learning framework that helps translate abstract conceptualizing into a process of going from everyday language to structured language to symbolic notation.
Intervention or Approach:The experiential learning model developed by David Kolb serves as the framework for the AP approach. Within this framework, the AP pedagogy has evolved an approach that centers on facilitating students’ understanding of mathematical concepts through the use of the experiences and the language they bring to the classroom. As a student-centered approach to teaching and learning, teachers are trained how to incorporate cooperative learning strategies that translate abstract conceptualizing into a process of going from everyday language to structured language to symbolic notation in a cooperative learning environment. The AP content modules use a series of demonstrations and hands-on experiences to concretize the abstract mathematical principles.
The Algebra Project’s curriculum is student-centered and grounded in 5 crucial steps based on a model of experiential learning which has proved so successful in middle and high schools (Moses & Cobb, 2001): (i) Physical events or experience, (ii) Pictorial representations/modeling of events, (iii) Intuitive language about the events – “People Talk”, (iv) Structured language about the events – “Feature Talk”, and (iv) Symbolic representation of the events. In most cases, students engage in each step in this process first individually, then in small groups, and finally in whole class discussions.
Products: Report | Algebra Project Website
 Algebraic Knowledge for Teaching: A Cross-cultural Perspective (NSF #1350068)
Algebraic Knowledge for Teaching: A Cross-cultural Perspective (NSF #1350068)
PI: Meixia Ding
Grades: K-5
Specific Content/Skills/Types of Reasoning Addressed: This project explores algebraic knowledge for teaching (AKT) in elementary school from a cross-cultural perspective. The targeted concepts include inverse relations and basic properties of operations.
Intervention or Approach: To identify the necessarily AKT, we conducted design-based research on expert teachers’ lessons of inverse relations (additive, multiplicative) and basic properties of operations (commutative, associative, and distributive). The targeted instructional aspects included using worked examples to enhance problem solving, connecting concrete and abstract representations, and asking deep questions to elicit students’ deep explanations all of which were supported by the cognitive load theory. Below are elaborations of the detailed activities:
During years 1-2 of the project, we examined expert teachers’ (Grades 1–4) classroom instruction in both the United States and China. Video analysis was used to identify which components of the expert teachers’ use of worked examples, representations, and deep questions, were most effectively linked to students’ achievement. Intensive data analysis across teachers, topics, and nations were conducted in year 3 to sort out a knowledge base of AKT, which were developed into teaching materials as project intervention.
To evaluate the identified AKT, we shared the preliminary findings with expert teachers in both countries through online video forums and summer workshops at the end of year 3. Teachers in both countries were asked to reteach the lessons in year 4. Lessons were videotaped, analyzed using the same coding scheme, and then compared with the videos collected in years 1 and 2 (we are now analyzing the year 4 data.) In all cases, changes in student achievement, controlling for confounding factors, will be considered. These findings will be used to inform the refinement of the identified AKT.
Key Challenge: During year 4 of the project, we noticed that teachers were more able to transfer some aspects learned from their international peers than others. For instance, many U.S. teachers purposefully incorporated strategies of situating worked examples in a real-world situation like their Chinese peers and successfully faded the concreteness in their lessons. However, we also noticed that asking deep questions to elicit students’ deep explanations remained a challenge. For instance, some teachers seemed to have superficial definitions for what depth means (e.g., having students describe computational strategies) while other teachers seemed to have issues with knowing when to probe further after an initial deep question. These observations call for further support for U.S. elementary teachers’ knowledge improvement. Future research may extend this project to enhance teachers’ AKT.
Theoretical Framework: As mentioned earlier, the theoretical framework we used to ground this research is cognitive load theory as indicated by three cognitive instructional principles: using worked examples to enhance problem solving, making connections between concrete and abstract representations, and asking deep questions to elicit students’ deep explanations.
Methodology: The methodological approaches of this project include design-based research and cross-cultural video analysis. Based on video analysis of U.S. and Chinese teachers’ initial classroom teaching, we identified essential features of AKT and developed a video-based project intervention in year 3. We then shared the findings with participating teachers through a one-month online video forum and a 20-hour summer workshop. Teachers who received the project intervention re-taught their lessons, which was informative for evaluating and refining the identified AKT. Research instruments from this project include a video coding frame and three student content tests. The video coding framework was adapted from a prior research publication on teachers’ lesson planning. The student instruments include one test for additive inverses, one for multiplicative inverses, and one for the basic properties of operations.
Products: NSF STEM for All Video Showcase Entries - 2015, 2016, 2018 | Publications | Presentations
Algebraic Learning and Cognition in Learning Disabled Students (NSF #1659113)
PI: David Geary
Grades: 6-9
Specific Content/Skills/Types of Reasoning Addressed: The 6th grade assessment includes a thorough evaluation of prerequisite procedural and conceptual competencies in whole number and fraction arithmetic, as well as understanding of mathematical equivalence. The 9th grade assessments will include experimental measures of students’ efficiency in processing algebra expressions, memory for the basic structure of algebra equations, understanding of coordinate space, and understanding of how functions map to this space. Tests of the students’ procedural competence in algebra and their skill at solving algebra word problems will also be assessed. Attitudes about mathematics and language arts will be assessed 4 times from 6th through 9th grade, as will mathematics anxiety. Mathematics and language arts teachers will complete surveys on each participants’ in-class attentive behavior in 7th, 8th, and 9th grade.
Students’ mathematics and reading achievement will be assessed in 7th to 9th grade, inclusive, and their cognitive ability in 7th grade. The 7th and 8th grade assessments will include evaluations of their working memory (ability to hold something in mind while doing something else) and verbal and visuospatial memories, as well more complex spatial abilities.
A subset of students will participate in a parallel qualitative study of their conceptual understanding of variables. In 7th, 8th, and 9th grade, the students will participate in clinical interviews structured around a series of variables questions.
Intervention or Approach: The project involves a 6th to 9th grade longitudinal assessment of the prerequisite (e.g. fractions), cognitive (e.g. working memory), and non-cognitive (e.g. mathematics anxiety) factors that dynamically influence students’ algebraic learning and cognition, with a focus on at-risk students. The study will be the most comprehensive assessment of the development of algebra competence conducted to date and is organized by an integrative model incorporating cognitive and non-cognitive influences on students’ engagement in mathematics classrooms and on the learning of procedural and spatial-related aspects of algebra.
Key Challenge: The most critical challenge is keeping students enrolled for the duration of the project, across 9 assessments over 3 years. The team is very experienced in organizing and conducting longitudinal studies and have been successful in keeping students enrolled in these projects, one of which spanned 10 years (kindergarten through end of 9th grade).
Theoretical Framework: The project has an overall cognitive science framing to it, with a focus on the relation between specific cognitive abilities, such as visuospatial working memory, and specific aspects of algebra competence, such as understanding how functions maps onto coordinate space. The approach goes beyond typical studies of this type, with inclusion of non-cognitive factors (e.g., mathematics anxiety) and in-class attentive behavior (based on teacher surveys). The goal is to also integrate results from the qualitative interviews and the quantitative assessments.
Methodology: The study includes a mix of quantitative and qualitative assessments. The cognitive and experimental algebra assessments are done with custom software that is implemented on iPads. These provide information on speed and accuracy of problem solving. Other assessments include standardized achievement and ability tests, and pencil and paper algebra tests. Most of these are administered one-on-one. The 6th grade assessments were conducted in mathematics classrooms and included a mix of iPad and pencil and paper assessments. The qualitative assessments are conducted in the lab’s mobile testing office (parked in front of the students’ home). These are videotaped and audiotaped for later analysis based on rubrics developed from pilot work.
Products: MU Math Study - Algebra Website | Upcoming Publication | 6th Grade Measures & Manuals for Cognitive Tasks
Assessing Secondary Teachers' Algebraic Habits of Mind (NSF #s 1222340, 1222426, 1222496)
PIs: Ryota Matsuura, Glenn, Stevens, Sarah Sword | Co-PI: Al Cuoco
Grades: 7-12
Specific Content/Skills/Types of Reasoning Addressed: Mathematical habits of mind (MHoM), i.e., the specialized ways of approaching mathematical problems and thinking about mathematical concepts that resemble the ways employed by mathematicians.
Intervention or Approach: The MHoM construct is closely aligned with the Common Core Standards for Mathematical Practice. Many of the Mathematics Teaching Practices in NCTM’s Principles to Actions depend on teachers’ MHoM for implementation. Thus, there is a growing national demand for teachers to acquire practices that are consistent with MHoM as part of their mathematical repertoire.
Through our work in teacher PD, we had seen that MHoM is a collection of habits teachers can acquire, rather than some static “either you have it or don’t” state of being. Teachers had reported that developing these habits had a tremendous effect on their teaching. They had described deeper knowledge of mathematics, changes in beliefs about the nature of mathematics and how students learn mathematics, renewed passion for mathematics, and changes in instructional practice. We had ample anecdotal evidence. But we wanted to test scientifically our hypothesis that these teachers developed MHoM and that these habits had an impact on their teaching practice. In addition, we wanted to measure the effects of our own PD programs using instruments that were consistent with our goals.
Thus we began investigating the question: What are the mathematical habits of mind that secondary teachers use, how do they use them, and how can we measure them?
To examine this, we operationalized our definition of MHoM, starting with algebra, and developed two instruments—a paper and pencil assessment and an observation protocol—that measure how teachers use MHoM while doing mathematics on their own and teaching mathematics to their students.
Products: Instruments | Papers & Presentations
Developing Pre-Service Teachers' Capacity to Teach Students with Learning Disabilities in Algebra I (NSF #1813903)
PI: Casey Hord | Co-PI: Anna DeJarnette
Grades: 9-12
Specific Content/Skills/Types of Reasoning Addressed: We target concepts and procedures related to linear functions, equations, and systems of equations, including the representations (graphs, tables, symbols) used to represent these objects.
Intervention or Approach: Mathematical proficiency can be defined as intertwining strands of knowledge and skills including conceptual understanding, procedural fluency, and productive disposition (Kilpatrick, Swafford, & Findell, 2001). We use the model of mathematical proficiency to describe the content knowledge that we intend for tutors to help students develop. We expect that tasks designed to promote procedural fluency (e.g., solving systems of equations using multiple methods) can be opportunities for tutors to promote conceptual understanding (e.g., discussing the meaning of equality or a rationale for substituting one expression for another). We hypothesize that improved conceptual understanding will support connections to long-term memory, thus overcoming challenges with working memory that make it difficult for students with learning disabilities to store and use multiple pieces of information on multi-step problems (Swanson & Siegel, 2001). Moreover, a productive disposition incorporates a student’s belief in his or her efficacy (Kilpatrick et al., 2001). We see the development of a productive disposition as essential for students with learning disabilities to overcome mathematics related anxieties and have opportunities to build conceptual understanding and procedural fluency.
Our intervention attends to tutors’ use of gestures and strategic patterns of questioning in order to foster the three intertwining strands of mathematical proficiency. We hypothesize that gesturing can support students’ working memory during procedural tasks and create opportunities to pose questions that focus students’ attention on important concepts. We further attend to how tutors might modify their questioning to respond to individual students’ dispositions, within individual tutoring sessions and over time.
Key Challenge: There is an ongoing need to improve opportunities for students with LD to be engaged and successful in science, technology, engineering, and mathematics (STEM) disciplines, and Algebra 1 is an important gatekeeper to STEM pathways. In our project, we are working to train pre-service teachers to support meaningful learning opportunities for students with LD. By measuring the long-term impact of that training on the pre-service teachers, this project has the potential to provide a sustainable model to better serve the needs of students with LD in mathematics and promote the development of highly effective teachers of students with LD.
Methodology: We have been conducting qualitative analyses of tutor training sessions for preservice teachers and sessions of tutors teaching high school students with learning disabilities. We will focus our attention on tutors’ attention to the use of gestures and different types of questions they use in tutoring session as well as the tutors’ learning during training sessions. In the long-term, we will document tutors’ growth and, also, compare tutors’ work in the field to their work in the training environment.
Products: Coming Soon! 2019 Conference Presentations & Other Products
Development and Empirical Recovery for a Learning Progression-Based Assessment of the Function Concept (NSF #1621117)
PI: Edith Aurora Graf | Co-PIs: Gregory Budzban, Robert Moses, Sarah Ohls, Peter van Rijn
Grades: 8-12
Specific Content/Skills/Types of Reasoning Addressed: Understanding of the mathematical concept of function.
Intervention or Approach: We developed a learning progression (LP) and assessment tasks for the concept of function, which is both central to algebra and challenging to understand. The LP focuses on three interrelated strands that correspond to different types of functions. The “traditional” strand assumes a brief introduction to the concept of function using finite-to-finite mappings, followed by a focus on real-valued to real-valued functions. The “finite-to-finite” strand focuses on mappings from finite sets to finite sets, and is aligned with the Algebra Project’s Road Coloring curriculum module. The “geometry” strand focuses on geometric transformations as functions, and is aligned with the Algebra Project’s Symmetries, Shapes, and Groups curriculum module. The unifying theme that ties the three strands together is the uniqueness property of a function—that each element of the domain is mapped to exactly one element of the range. Our rationale for developing a three-stranded progression is that the concept of function is best learned through experience with all these function types. An important goal of our project was to design tasks that were both aligned to the LP and attentive to the language and culture of a diverse body of students. To this end, we incorporated student voice into the task design, through focus groups and cognitive interviews conducted with young people by staff of the Young People’s Project. At this point in the project, a pilot administration of the tasks on computer has just been completed, and we are preparing to score responses using levels of the LP.
Products: Video (2019) | Video (2020) | CADRE Technology-Enhanced Assessment Feature
 Flipped Math Study (NSF #1721025)
Flipped Math Study (NSF #1721025)
PI: Zandra de Araujo | Co-PIs: James Tarr, Ze Wang, Samuel Otten
Grades: 8-10
Specific Content/Skills/Types of Reasoning Addressed: The project’s focus is on key concepts and procedures in algebra including understanding of variables and expressions, and solving equations.
Intervention or Approach: Flipped instruction is a model of instruction in which teachers typically deliver content via video prior to in-class practice and application. The use of flipped instruction is largely a teacher-initiated adoption and, to date, teachers’ use of this instructional model has outpaced research. We wanted to understand how teachers are using flipped instruction, particularly in algebra. We chose algebra because it is typically taught with an emphasis on procedures and rules. This focus on procedures and rules means that content can be offloaded to delivery via video. Moreover, high school algebra continues to serve as a gatekeeper to higher level mathematics. As such, we hypothesized that teachers might choose new approaches to teaching algebra, such as flipped instruction.
We are studying instructional formats utilized by teachers who flip their algebra instruction. In particular, we are examining the types of tasks, grouping formats, videos, and student engagement in flipped and non-flipped algebra courses and possible correlations between these aspects and student learning outcomes. At the conclusion of our study, we should have a better idea of aspects of instruction that may be promising with regard to flipped instruction. Also, because we are collecting student survey data, we will also build a better understanding of students’ views on this instructional model.
Key Challenge: Student consent rates are an ongoing challenge of classroom-based research. Perhaps unsurprisingly, it is often difficult to get teenagers to return to consent forms. Also, students don’t always remain in the class or school in which they start the school year. These realities make doing matched pre/post over the course of an entire school year quite difficult. It’s also a challenge to decide upon what to assess in order to get a good idea of algebra learning throughout an entire year and across different teachers who utilize a variety of curricula.
Theoretical Framework: Theoretically, we are grounding our research in a sociocultural perspective. Taking this perspective means that we were interested in the social and individual dimensions of mathematics. Moreover, we find it necessary to consider the student interaction and engagement in mathematics classrooms as an aspect of mathematics instruction and learning.
Conceptually, our work builds on the framework we developed in our pilot work and refined in the first two years of this study (see attached paper on the framework for more information).
Methodology: We are utilizing both qualitative and quantitative methodologies for our study. In terms of the quantitative analysis, we are conducting a correlational analysis with multi-level modeling to examine student learning over the course of Algebra 1 instruction. In terms of qualitative analysis, we are utilizing case studies of particular classes. For example, we are writing a paper on a flipped teacher and non-flipped teacher who taught the same lesson in the same building. This study allows us to tease out the differences and similarities of the lessons.
Products: Presentations & Publications | Framework for Flipped Math Instruction | Observation Protocol Description | Poster
Investigating Differentiated Instruction and Relationships between Rational Number Knowledge and Algebraic Reasoning in Middle School (IDReAM) (NSF #1252575)
PI: Amy Hackenberg
Grades: 7-8 (relevant to 6-9)
Specific Content/Skills/Types of Reasoning Addressed: We study relationships between students’ rational number knowledge and algebraic reasoning with a focus on quantitative unknowns, equations and equivalence, distributive reasoning, and proportional reasoning.
Intervention or Approach: Students come to middle school with three broad ways of organizing numbers and quantities into units, where units are 1s or measurement units like inches. We refer to these ways of thinking as students’ multiplicative concepts; transitioning between them requires significant learning that can take a couple of years. Students’ multiplicative concepts influence their understanding of many topics relevant to middle school, such as fractions, integers, and algebra. So, we use these concepts to frame students’ diverse ways of thinking and to guide our teaching.
Research has shown that students with the first two multiplicative concepts need to enact their reasoning more extensively than students with the third. That means that these students need to act out materially or in visualized imagination the work they do in solving problems. In contrast, students with the third multiplicative concept can often thematize their ideas more quickly.
In our project, we conduct design experiments with small groups and whole classrooms. First, we construct initial models of the thinkers and pose problems that fit with these models and that could provoke learning. Second, we regularly ask students to represent their reasoning with drawings, using software such as JavaBars (Biddlecomb & Olive, 2000). Third, we regularly ask students to explain and present their reasoning. Fourth, we use on-going formative assessment to hone our understanding of students’ cognitive characteristics and help students become aware of what they know. These features facilitate students’ needs for enacting and thematizing, supported by small and large group discussion.
Key Challenge: The topic we are engaged in is a pervasive challenge in the field of Mathematics Education, and in education more broadly, which is how to handle diversity in classrooms. In the US, a traditional response to diversity at the secondary level is tracking, where students are slotted into different pathways of courses so that students who think similarly might be taught together. The main rationale is that it will be easier to teach students together who have developed similar ideas.
There are at least three problems with this approach. First, all teachers know that even students in the same tracked class (e.g., “regular” sixth grade math) are quite diverse in their thinking. Second, low-achieving students are often placed in classes that emphasize rote learning and do not allow movement to classes with high-achieving peers (Boaler, Wiliam, & Brown, 2000; Stiff, Johnson, & Akos, 2011). Third, and most pernicious, recommendations for class placements have been found to be biased against promoting students of color to advanced classes (Flores, 2007; Rubin, 2006; Stiff, et al., 2011), creating significant opportunity gaps (Flores, 2007). In response to such issues, the National Council of Teachers of Mathematics (NCTM, 2018) recently recommended that high schools discontinue tracking in mathematics.
Differentiating instruction for students with diverse ways of thinking in one classroom is a promising idea, but it is extremely hard to implement in a sustained way. Understandably, teachers are concerned about several issues, including increased workload (Tobin & Tippett, 2014), management of the classroom environment when students are engaged in different activities (Tomlinson, 1995), fairness of different work and support for students (Hockett, 2010), and management of formative assessment data and varied student assignments (Simpson, 1997). Currently the main way to handle that is to help teachers see that they can engage in “lower prep” strategies as well as help them understand “higher prep” strategies so that they can start small (Tomlinson, 2005); to help them see that while differentiating instruction does ultimately involve significant renovation in teaching practices to be done well, it can start with implementing a few strategies, being committed to getting to know students’ thinking, and being open.
Theoretical Framework: The PI uses radical constructivism (von Glasersfeld, 1995) in her work, complemented by complexity theory (Davis & Sumara, 2006).
Methodology: We use design experiment research (Cobb, Confrey, diSessa, Lehrer, & Schauble, 2003), as mentioned above.
Products: Video | Publication | NCTM Presentation | Coming Soon! Materials for Prospective Teachers & Additional Publications
LEAP V: Identifying Effective Instructional Practices that Foster the Development of Algebraic Thinking in Elementary School (NSF #1721192)
PI: Eric Knuth | Co-PIs: Maria Blanton, Angela Gardiner, Ana Stephens, Despina Stylianou
Grades: 3-5
Specific Content/Skills/Types of Reasoning Addressed: Practices of generalizing, representing, justifying, and reasoning with mathematical structure and relationships across content strands related to mathematical equivalence, generalized arithmetic, and functional thinking.
Intervention or Approach: The project team is examining videos of Grades 3-5 classroom teachers implementing an early algebra intervention, and identifying profiles of instructional practice that are linked to student performance on end-of-year early algebra assessments. The early algebra intervention that serves as the context for this research was developed as part of Project LEAP (a series of federally-funded projects focused on early algebra). The video data were collected as part of a large-scale, cluster randomized study to test the effectiveness of the early algebra intervention (approximately 4500 students from 46 schools); the intervention consisted of approximately 20 1-hour early algebra lessons per grade level (see Blanton, Stroud, Stephens, Murphy Gardiner, Stylianou, Knuth, Isler-Baykal, & Strachota, In press). Video data were collected from a random sample of approximately 45 teachers per grade level. The grade level observation data will be analyzed using latent profile analysis in order to identify profiles of instructional practice and to relate latent profile membership to distal student performance outcomes (i.e., performance on the early algebra assessments).
Key Challenge: A primary challenge associated with our project relates to the universally held belief that the nature of teachers’ instructional practices significantly affects the nature of students’ learning. Despite the commonsense of this belief, however, research evidence that links instructional practices with positive student outcomes is surprisingly lacking. Consequently, our work not only directly addresses this challenge, but also holds promise to offer practical guidance to teacher leaders, teacher educators, and teachers to support the development of instructional practices that may enhance the algebraic knowledge and skills of elementary students.
Product: Upcoming Publication
Measuring Early Mathematical Reasoning Skills: Developing Tests of Numerical Relational and Spatial Reasoning (MMaRS) (NSF #1721100)
PI: Leanne Ketterlin Geller | Co-PI: Lindsey Perry
Grades: K-2
Specific Content/Skills/Types of Reasoning Addressed: The project will develop and evaluate the validity of classroom assessment tools focused on foundational constructs for future mathematics performance, numeric relational reasoning and spatial reasoning.
Intervention or Approach: The importance of early mathematics to future achievement cannot be overstated. In fact, early mathematics is a better and more powerful predictor of future learning, including reading and mathematics achievement, compared to early reading ability or other factors such as attention skills (Duncan et al., 2007). In the MMaRS project, we target Numeric relational reasoning and spatial reasoning, two constructs that are important to and predictive of future success in mathematics (Aunio & Niemivirta, 2010; Friedman, 1995), and spatial reasoning in particular is predictive of STEM career and college degree selection (Uttal & Cohen, 2012; Wai, Lubinski, & Benbow, 2009). Currently, teachers do not have classroom assessment instruments that assess these constructs in Grades K-2.
As part of the data use cycle (Hamilton et al., 2009), teachers need high quality assessment tools from which to make sound instructional decisions. When teachers have data about their students’ prior knowledge and current understanding, they can design instruction that builds on students’ strengths and addresses their needs. MMaRS is intended to support teachers with a suite of classroom assessment tools so that they have data on students’ numeric relational reasoning and spatial reasoning from which to design effective instruction and intervene early for students who need extra support. We integrate the principles of universal design (Ketterlin-Geller, 2005) to develop tools that are free from bias and accurately capture all students’ reasoning skills. With these tools, teachers can provide the support for all students to be successful in mathematics now, so that they remain on this trajectory throughout their school and later careers.
Products: NCTM Presentation | PMENA Presentation | RCML Poster | Video
 Project LEAP: Learning through an Early Algebra Progression (Suite of NSF Funded Projects, Including NSF #1720129)
Project LEAP: Learning through an Early Algebra Progression (Suite of NSF Funded Projects, Including NSF #1720129)
PI: Maria Blanton | Co-PIs: Angela Gardiner, Eric Knuth, Ana Stephens, Rena Stroud
Grades: K-5
Specific Content/Skills/Types of Reasoning Addressed: Project LEAP targets the development of core algebraic thinking practices of generalizing, justifying, representing, and reasoning with mathematical structure and relationships across diverse content domains.
Intervention or Approach: Our team designed an early algebra curriculum for Grades K–5 that integrates core algebraic thinking practices of generalizing, justifying, representing, and reasoning with mathematical structure and relationships into the “Big Ideas” of generalized arithmetic; functional thinking; and equivalence, expression, equations, and inequalities—that is, content areas where these practices can occur.
The curriculum’s design uses a learning progressions approach (Clements & Sarama, 2004) that incorporates empirical, classroom-based research on levels of growth in children’s thinking about algebraic practices and concepts. Learning progressions, which are increasingly endorsed for their potential to inform the design of coherent standards, curricula, assessment, and instruction (Daro, Mosher, & Corcoran, 2011), provide an important research paradigm for our work.
The intervention consists of a sequence of 18–20 lessons for each of Grades K–5, along with grade-level assessments to measure students’ learning. Lessons begin with a brief “Jumpstart” to review previous concepts or prompt students’ thinking about new concepts, then transition into small-group investigations in which students explore concepts that engage them in core practices and concepts. They conclude with a whole-group discussion of students’ findings and a “Review and Discuss” that serves as a formative assessment. Lessons emphasize the development of meaning for algebraic ideas by engaging students in explaining and justifying their thinking, both orally and in writing.
 Key Challenges:
Key Challenges:
- Understanding how to design curriculum and the tools needed in order to more fully address the needs of students with learning differences or learning disabilities. We are currently conducting a DRK-12 research project that attempts to understand how attributes of lessons and specific tools support students who might struggle with early algebraic concepts.
- Successfully engaging teachers—and school and districts more broadly—in early algebra so that it (and STEM, in general) is on equal footing with literacy. This includes helping stakeholders understand the importance of early algebra, that the lack of attention to it will impact students in later grades in deep and significant ways, that it is learnable (and their own fears of algebra need to be addressed), and that arithmetic is not fully understood until the algebraic character of arithmetic is understood (that is, it does not make good mathematical sense to treat arithmetic and algebra as disjoint content). Through a DRK-12 project, we are currently trying to identify models of practice enacted by teachers who exhibited high fidelity of implementation of our intervention for Grades 3 – 5.
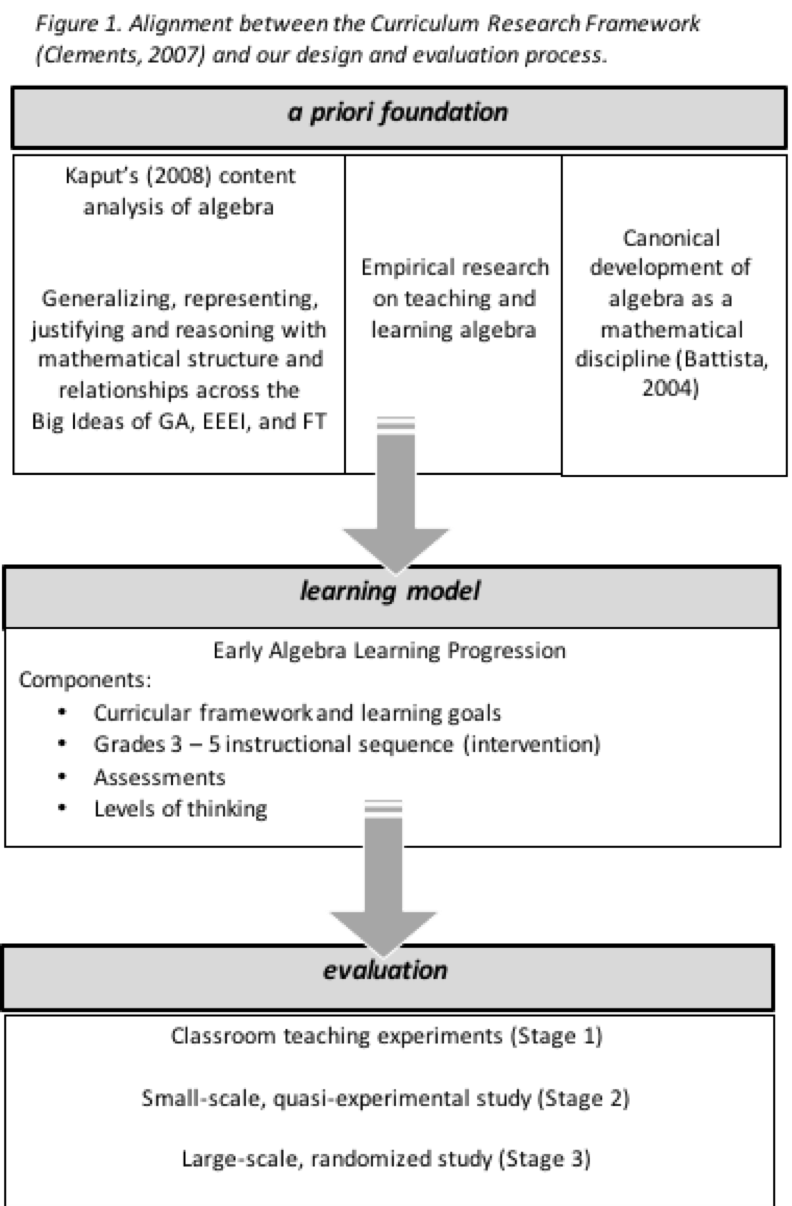
Theoretical Framework & Methodology: We base our approach to algebra on Kaput’s (2008) content analysis of algebra as a set of core practices within several key strands. Building from his framework, we conceptualize early algebra as a set of 4 different practices (generalizing, representing, justifying, and reasoning with mathematical structure and relationships) within 3 key content domains or “Big Ideas” (generalized arithmetic; functional thinking; and equivalence, expression, equations, and inequalities).
We used a learning progressions approach as a research paradigm for our overall curricular design. This includes that our curricular innovation included (1) learning goals, (2) an instructional sequence designed to achieve these goals, (3) assessments that measure learning as students progress along the sequence, and (4) levels of sophistication in students’ thinking as they advance through the sequence (Clements & Sarama, 2004).
In general, our design and evaluation process aligns with the Curriculum Research Framework identified by Clements (2007). Figure 1 captures the key components of our work and their alignment with this framework.
Products: Curriculum | Project Websites - TERC, UW Madison | Publication | PI Interview
 Teaching and Learning Algebraic Thinking with PhET Interactive Simulations (NSF #1503510)
Teaching and Learning Algebraic Thinking with PhET Interactive Simulations (NSF #1503510)
PI: Katherine Perkins | Co-PIs: David Webb, Ian Whitacre, Karina Hensberry
Grades: 6-9
Specific Content/Skills/Types of Reasoning Addressed: Conceptual content (e.g. proportions, unit rates, expressions, functions, (in)equality) and mathematical practices (e.g. discovering patterns/relationships, using models, reasoning/argumentation)
Intervention or Approach: This research and development project is investigating the design and classroom use of rich, exploratory, interactive simulations and associated instructional materials to advance algebraic thinking in Grades 6-9. The project builds on the community's solid foundation of knowledge in mathematics education technology, and focuses on how, through simulation design and lesson design, to 1) engage students in authentic mathematical reasoning as they use technologies, 2) support teachers to use pedagogically-effective, sim-based instructional approaches, and 3) reduce barriers to the adoption and spread of research-based technologies by mathematics teachers.
The theory of change is anchored in the transformational potential of interactive simulations. These simulations: are dynamic and highly interactive; can scaffold and cue inquiry by what is displayed and what is controlled; link multiple representations; highlight conceptually important relationships and patterns; and support rapid inquiry cycles. Many simulations leverage progressive formalization, bridging from concrete representations to mathematical abstractions. Together, these features enable immediate and specific feedback, provide flexibility to pose questions, test ideas, and reason abstractly, and enable the sim to take on routine tasks (e.g., computations), allowing students to identify patterns, make generalizations, and focus deeply on concepts.
The insertion of a simulation into the classroom opens up new opportunities for students to have increased agency and to discover key mathematical ideas, and for teachers to shift from a role as ‘the source of knowledge’ to one as ‘the critical guide and facilitator’ engaging students in the mathematical practices and content understanding.
Key Challenge: Our survey of mathematics teachers adopting PhET simulations shows that mathematics teachers cite limited flexibility and time in their schedule as a barrier to bringing simulations into their classrooms. Teachers have rated the simulation-specific lessons and lesson plans available at the PhET website as very helpful and report using them most often of our various teacher resources.
In addition, our classroom research observed teacher facilitation practices during sim-based lessons and documented teachers experiencing a tension between supporting student agency through simulation play and directing students to achieve specific learning goals. We provided instructional strategies for balancing these priorities (Whitacre et al., 2019).
Theoretical Framework: We have used a variety of theoretical lenses to understand and examine the role of interactive simulations in shaping teaching and learning in the mathematics classroom. For instance, since the design of the PhET mathematics simulations embodies several principles of Realistic Mathematics Education (van den Heuvel-Panhuizen & Drijvers, 2014), we have used this as a framework to analyze task design and use, and examine the ways in which students and teachers use and discuss sim-supported mathematics activities in their classroom. Three RME principles, in particular, have been used in our analysis of PhET sims, instructional materials, and research data: the reality principle (i.e., use of realistic contexts to develop and explore mathematics), the activity principle (e.g., positioning students as active learners in making sense of mathematics), and the level principle (i.e., progressive formalization). In Realistic Mathematics Education, students are empowered as learners in an iterative process through which they form their own constructions and productions (Streefland, 1991). Students need to form their own understandings and construct meaning behind what they are doing, not just be told how a process works and expected to repeat it in new contexts when needed.
In another research study, we are using foundational ideas by Boaler (2003) and Cobb et al. (2009) to examine social and sociomathematical norms in the sim-based classroom. Boaler (2003) suggests examining the “recurrent activities and norms that develop in classrooms over time, in which teachers and students engage”. Cobb et al. (2009) describes an interplay between authority and agency that influences the nature of agency (conceptual or disciplinary) existing in the classroom. We build on these perspectives to investigate collective activity involving simulations in mathematics classrooms and examine whether instruction incorporating simulations may support different social and sociomathematical norms that are not available in normal, non-sim lessons.
Methodology: This project includes individual student interviews, teacher interviews, and studies of classroom implementation through observation with analysis of video recordings. Interviews are used to examine simulation usability, engagement, and achievement and to identify simulation design approaches that stimulate productive use. Classroom-based studies investigate how simulations can be combined with instructional materials and teacher facilitation to engage groups of students in inquiry, promote rich discussions of important mathematical ideas, and advance achievement of Common Core State Standards for Mathematics.
Classroom studies have examined a range of teacher use of simulations and also compared across a variety of implementations of sim-based instruction as well as to business-as-usual instruction. Data collection has included classroom video, student worksheets, pre-post content measures, student attitude surveys, and teacher surveys and pre-post teacher interviews. The Instructional Quality Assessment (IQA) framework and the Mathematical Quality of Instruction (MQI) framework have been employed for the comparative analysis of sim-based instruction to business-as-usual instruction, identifying observable indicators of high-quality mathematics instruction. Other methodological approaches are as described in project papers.
Finally, online surveys and teacher logs have been employed to evaluate broader teacher uptake and use of these mathematics simulations, including questions and analysis to characterize the nature and goal of teachers’ use as well as barriers to use that teachers experience.
Products: Free Interactive Simulations for Math | Simulation-Based Lessons & Teacher Tips | Exemplar Math Lesson - Defining Functions | Theory of Change Model | Sample Publications
 Using Math Pathways & Pitfalls to Promote Algebra Readiness (NSF #1314416)
Using Math Pathways & Pitfalls to Promote Algebra Readiness (NSF #1314416)
PI: Jodi Davenport | Co-PIs: Yvonne Kao, Alma Ramirez
Grade: 7
Specific Content/Skills/Types of Reasoning Addressed: This project targets key misconceptions, or pitfalls, that prevent middle schoolers from developing a deep conceptual understanding of algebra.
Intervention or Approach: Math Pathways & Pitfalls Algebra Readiness lessons are designed to be used to supplement any adopted textbook and are aligned to the 7th grade Common Core State Standards for Mathematics. During lessons, students engage in mathematical discussions and tackle mathematical pitfalls. Each lesson spans two days and is accompanied by teaching guides that provide sample discussion prompts and other supporting material.
On Day 1, students review the Purpose of the lesson and key Math Words that will likely come up in discussions. Students engage with a Starter Problem that often elicits pitfalls from students. They discuss two fictional students’ approaches to the Starter Problem—one correct, or “OK” approach, and one approach that contains a pitfall. Day 1 concludes with an additional Practice problem, Things to Remember, and Reflection.
Day 2 opens with a review of Day 1. Then students work in pairs on three problems that extend their thinking beyond the problems from Day 1, discussing their work with the whole class at the end of each problem. Students examine an “OK” solution from a fictional student and answer a question to show they understood the fictional student’s work. Students grapple with a Pitfall solution, explain why it doesn’t make sense, and find a correct solution. Students then engage with a third problem, which may be partially-worked, to further extend their thinking. Teachers can further reinforce the concepts from the core lesson by assigning additional problems.
Key Challenge: Enhancing teachers’ pedagogical and mathematics content knowledge for facilitating productive classroom discourse is a pervasive challenge in this type of work. Teachers must be able to anticipate student responses, select examples of student work would drive a productive mathematical discussion, and possess a deep enough understanding of the concept to help students unpack and highlight the key mathematical connections. The Math Pathways & Pitfalls Algebra Readiness team addresses this challenge by including sample discussion prompts, mathematical insights, and teaching tips in the teaching guides. The DRK-12 project also included 4-day professional development institutes, which guided participating teachers through the content of selected lessons and provided a structure for planning for the discourse in each lesson.
Theoretical Framework: Math Pathways & Pitfalls is organized around five research-based principles for how children learn mathematics, and specific teaching practices for enacting each principle in the classroom:
- Building mathematical discussions. Using academic language to reason about, explain, and justify mathematical ideas builds understanding and the capacity to make mathematical arguments.
- Making sense. Making sense of the mathematical meaning of words, symbols, and diagrams in contextualized and decontextualized problems is fundamental to finding and evaluating solutions.
- Confronting pitfalls. Contrasting mathematical reasoning with and without pitfalls builds conceptual understanding and prompts students to self-monitor and self-correct.
- Visualizing and connecting. Discussing relationships among mathematical ideas using visual, verbal, and symbolic representations builds robust conceptual understanding.
- Capturing key ideas. Creating a strategic public record of key mathematical ideas as they are being discussed helps students understand, summarize, and remember those ideas.
Methodology: The Math Pathways & Pitfalls Algebra Readiness lessons have been developed and field-tested over three years by public and charter school teachers in California. Field test data included classroom observations and teacher interviews and teachers’ responses on weekly teaching logs. The lessons were revised after each year to incorporate feedback from the field test and feedback from a panel of expert reviewers. In addition, the project examined associated changes in field test teachers’ mathematics knowledge for teaching and beliefs about teaching mathematics.
Products: Curriculum with Teacher Guide & Student Pages
 Video in the Middle: Flexible Digital Experiences for Mathematics Teacher Education (NSF #1720507)
Video in the Middle: Flexible Digital Experiences for Mathematics Teacher Education (NSF #1720507)
PI: Nanette Seago | Co-PIs: Catherine Carroll, Robert Montgomery
Grade: 6
Specific Content/Skills/Types of Reasoning Addressed: Mathematical knowledge for teaching linear functions, expressions and equations, with a focus on linking mathematical representations, examining student reasoning and multiple solution methods.
Intervention or Approach: WestEd will design and develop a web-based form of professional development/teacher education. Video in the Middle (VIM): Flexible digital experiences for mathematics teacher education will produce a collection of 40 VIM modules that can be experienced in reasonable bite sizes, varied sequences, and in flexible collaboration formats to meet a critical need for professional learning that is personalized, ongoing, job-embedded, and collaborative. The VIM project will support the ongoing introduction of dynamic new math content with video examples of practice and, most importantly, ongoing application and reflection protocols for impacting classroom instruction.
The design of each VIM module places a video clip at the center, or “in the middle,” of an online professional learning experience for teachers. The full VIM module experience includes mathematical problem solving, video analysis of classroom practice, and pedagogical reflection. Each individual VIM module will be comprised of approximately two hours of teacher learning time plus classroom application.
The VIM modules will be offered in three different digital delivery formats: (1) individual self-paced, (2) group-paced, and a (3) facilitated course of VIMs. We believe each of these formats has unique affordances for teachers which we will assess in this project. Ultimately, we believe teachers and teacher educators need the flexibility that comes with a wide collection of high-quality VIMs that can be accessed individually or in sequenced pathways based on a teacher or site's needs. The VIM project will examine the relative benefits of these delivery formats.
Key Challenges:
- Designing two-hour modules to impact teacher learning and instructional practice.
- Designing modules to fit use in three formats: Independent, locally facilitated and professionally facilitated.
Theoretical Framework: Situative theory suggests that learning is situated in a particular context, socially organized, and distributed across individuals, artifacts and tools (Putnam & Borko, 2000). Using classroom video in PD situates teacher learning firmly within their everyday routines of practice. In addition, the task of analyzing and making sense of video presents a high degree of complexity, providing teachers with motivation to socially engage and interact cooperatively (Blomberg et al., 2013). Hatch, Shuttleworth, Jaffee and Marri (2016) propose three elements that shape teachers’ learning from video in a professional development setting: (1) properties or affordances of the videos, (2) the background knowledge and experiences that teachers bring to the PD, and (3) social factors and activities in which videos are viewed and discussed by the participating teachers. They argue, “…the situated perspective highlights that the affordances for learning from video emerge from the interaction of all three” (pg. 276). In other words, situative theory helps make clear that teacher learning from a given video-based PD occurs as a result of the relationship between selected video representations of teaching, participants’ unique backgrounds, and socially organized viewing experiences.
Methodology:
Pathway Testing: During 2019-2020, we will test out interest in the bank of 25-35 modules with PD providers, teachers and preservice educators by organizing the modules with descriptive titles, learning goals, grade level and video description. We will use data analytics to examine which choices people make, in which order they do so, and their rationale for choices to determine different potential effective sequences of modules in preparation for dissemination.
Pilot Study: We will study three conditions in. which teachers will experience four VIM modules: Independent/Individual users (30); WestEd facilitated (30); Locally facilitated (30). Teachers will be randomly assigned at the teacher level into each condition. We will draw from 2 districts for the individual teachers and 5 districts for the two facilitated groups. In addition, we will randomly select 10-15% of teachers from each condition to observe instructional practice. The pilot study will occur in February-March 2020. Data to be collected: Online Artifact Analysis measure (math task, video analysis and student work analysis), weekly teacher logs, student quiz, SBAC student data. and classroom observations and interviews.
Products: Video| Publications