
In this Spotlight...
- Featured Projects
- Animated Contrasting Cases to Improve Procedural and Conceptual Knowledge in Geometry (AC²inG) (PI: Erin Krupa)
- Building Informed Designers (PI: Blake Hylton)
- CAREER: Noticing and Using Students’ Prior Knowledge in Problem-Based Instruction (PI: Gloriana González)
- COnceptual Model-based Math Intervention Tutor (COMMIT) (PI: Yan Ping Xin)
- DEAP: Developing and Evaluating Assessments of Problem Solving (PIs: Jonathan Bostic, Toni Sondergeld)
- Ed+gineering: An Interdisciplinary Partnership Integrating Engineering into Elementary Teacher Preparation Programs (PI: Jennifer Kidd)
- FLECKS: Fostering Collaborative Computer Science Learning with Intelligent Virtual Companions for Upper Elementary Students (PIs: Kristy Boyer, Eric Wiebe)
- Improving Grades 6-8 Students' Mathematics Achievement in Modeling and Problem Solving through Effective Sequencing of Instructional Practices (PI: Joe Champion)
- Mathematical and Computational Methods for Planning a Sustainable Future (PS-Future) (PI: Margaret Cozzens)
- Mathematical Learning via Architectural Design and Modeling Using E-Rebuild (PI: Fengfeng Ke)
- Proportions Playground (PI: Chandra Orrill)
- Science and Engineering Education for Infrastructure Transformation (PI: Charles Xie)
- Systemic Transformation of Inquiry Learning Environments for STEM (PI: Ellen Meier)
- Zoombinis: The Implementation Research Study of a Computational Thinking Game for Upper Elementary and Middle School Learners (PI: Jodi Asbell-Clarke)
- Additional Resources
Featured Projects
Animated Contrasting Cases to Improve Procedural and Conceptual Knowledge in Geometry (AC²inG) (NSF #1907745)
PI: Erin Krupa | Co-PI: Jon Star
Target Audience: Middle school students and teachers
STEM Discipline: Mathematics
 Description: Have you ever tried to identify the type of poison ivy in your yard? Or tried to teach a one-year-old the difference between red and blue? Often this learning occurs by directly comparing the poisonous leaf to ones in a magazine or showing the child something blue along with something red. Comparing and contrasting objects is a powerful learning tool with deep roots in cognitive science. The purpose of our research is to design curricular materials for geometry that focus on comparing different approaches to solving the same problem, and to examine the effects of these materials on student learning. Our goal is to improve students’ procedural and conceptual knowledge of geometry.
Description: Have you ever tried to identify the type of poison ivy in your yard? Or tried to teach a one-year-old the difference between red and blue? Often this learning occurs by directly comparing the poisonous leaf to ones in a magazine or showing the child something blue along with something red. Comparing and contrasting objects is a powerful learning tool with deep roots in cognitive science. The purpose of our research is to design curricular materials for geometry that focus on comparing different approaches to solving the same problem, and to examine the effects of these materials on student learning. Our goal is to improve students’ procedural and conceptual knowledge of geometry.
In our materials, two fictional students each present a unique solution strategy to a geometry problem. Middle school students analyze both methods and discuss similarities, differences, strengths, and weaknesses of each strategy. This research is based on positive outcomes of using contrasting cases to support the learning of algebra. The AC2inG project tests the conjecture that utilizing contrasting cases is a viable strategy for improving the learning of geometry. Further, AC2inG materials will be digital, so students will see the concepts come to life through rich visual animations.
Theoretical Framework:
- Multiple Solution Strategies: Mathematics education literature often advocates for the use of multiple solution strategies or tools to approach a mathematics problem (Dhombres, 1993; House & Coxford, 1995; NCTM, 2000; Polya, 1973, 1981; Pólya, 1963; A. H. Schoenfeld, 1983, 1988; Vinner, 1989).
- Contrasting Cases as Learning Tool: Goldstone, Day, and Son (2010) stated, “research has demonstrated that the simple act of comparing two things can produce important changes in our knowledge” (p. 103). There is empirical support from cognitive scientist literature for the use of comparing contrasting examples for learning about business negotiations (Gentner et al., 2003), heat flow in science (Kurtz et al., 2001), children’s learning (Loewenstein & Gentner, 2001; Namy & Gentner, 2002), and in studies of infants 4 to 6-months old (Oakes & Ribar, 2005).
- Contrasting Cases in Mathematics Education: In mathematics education, research on comparing has proven effective in learning: estimation (Star & Rittle-Johnson, 2008, March, 2009), the concept of an altitude for a triangle (Guo & Pang, 2011), and equation solving (Rittle-Johnson & Star, 2007, 2009; Rittle-Johnson, Star, & Durkin, 2012). Aside from the work of Star and colleagues, there are very few experimental classroom-based studies on the effects of the Contrasting Cases approach on gains in students’ knowledge, and only one such study exists in geometry (Guo & Pang, 2011).
Methodology: Overall, we are utilizing design-based research as we develop and test the materials (Brown, 1992; Cobb, Confrey, diSessa, Lehrer, & Schauble, 2003; Collins, 1992; Schoenfeld, 2006). We used a theory-driven process to design our materials and will use a data-driven process to iteratively refine them (Shavelson & Towne, 2002). Through a series of revisions and implementations, we will test and refine our conjectures about how, and what, students learn when interacting with the geometry cases, with the ultimate goal of improving their procedural and conceptual knowledge.
To obtain the data that will inform our revisions, we will use a quasi-experimental design that is similar to prior Contrasting Cases work in algebra (e.g., Rittle-Johnson & Star, 2007); half the students will be in the Sequential group and the other half in the Compare group. The Sequential group will be presented with a page with one student’s solution to a problem, a discussion sheet, a separate page with another student’s solution, and a second discussion sheet. The Compare group will be presented with the supplemental curriculum that includes: a page with one student’s solution to a problem, a page with another student’s solution to a problem, an in-depth side-by-side comparison sheet of the two solutions, a discussion sheet, and a ‘closure’ page.
All students will be administered lesson-level, unit-level, and course-level pre- and post-assessments. In addition, students will be allowed to write or draw on the AC2inG instructional materials, and all lessons will be audio-recorded. After instruction with the animated contrasting cases, we will conduct and audio-record interviews with small groups of students in order to explore students’ geometric thinking. A mixed-methods approach will be used to analyze the data that is collected in order to provide evidence of effectiveness of the supplemental materials on students’ procedural and conceptual knowledge of geometry.
Current Findings Related to Problem Solving: We are in the first of three years of the grant. To date, we have created paper-based curricular materials for all 8th grade geometry units: Angles, Volume, Transformations, and Pythagorean Theorem. We have created animation scripts that are currently under the third round of revisions with our digital animator, and we hope to have these finalized in time for the 2020-2021 school year.
Key Challenge: The most obvious current challenge is the COVID-19 pandemic. When schools closed, we were unable to implement our materials with students. To overcome this, we are prepared to conduct think-aloud interviews with students engaging in our digital materials once those have been finalized.
Products: Project Website | Curricular Materials
Building Informed Designers (NSF #1812823)
PI: J. Blake Hylton | Co-PIs: Todd France, Patrick Herak, Bruce Wellman
Target Audience: Grades 9-12
STEM Discipline: Infusing engineering content into physics, chemistry, biology, and physical science curricula
Description: This project is developing engineering problem framing activities for high school science classrooms and associated professional development for teachers. Teacher participants are brought in for a three day workshop, where they receive training on engineering content, complete an engineering design experience, walk through the materials, and work to develop an implementation plan for connecting the engineering content to their regular science content. Teachers meet with a team member for continued mentorship at least twice more as they work to enact their implementation plan. Curricular materials are currently undergoing a transformation towards a hybrid synchronous/asynchronous mode using interactive modules deployed via LMS. Materials are being developed for several different problem contexts, to allow tailoring to regular course content, and with multiple levels of proficiency, to allow students to revisit similar content at a higher level in later courses in the curriculum. In addition to analyzing student artifacts, the project also captures student attitudes about engineering as a career path, using the STEM-CIS instrument, and about engineering design, using a modified version of an established instrument based on expectancy-value theory. The project goal is to explore how students' attitudes and abilities shift through repeated exposure across the high school curriculum.
Theoretical Framework & Methodology: Student attitudes about engineering design are explored using a survey based on expectancy-value theory. Artifacts are coded to identify key traits and correlated with survey results. Students are also surveyed using the STEM-CIS to explore interest in engineering as a career path. In both cases, trends are examined over time as students encounter additional interventions throughout their high school curriculum.
Key Challenges: There have been two core challenges encountered on this project. First, cooperation of the district professional development coordinator is critical to ensuring access to teachers. We have learned that a formal documentation of this agreement and the expectations as to when teachers will be allowed to participate in project-related activities rather than district mandated activities is critical to success. Second, our initial model for the modules has changed significantly, in part due to observations during piloting and in part due to COVID-19. This has delayed publication of findings and materials.
Products: We hope to have a full suite of field-tested modules available next year.
CAREER: Noticing and Using Students’ Prior Knowledge in Problem-Based Instruction (NSF #1253081)
PI: Gloriana González
Target Audience: High school geometry, high-need schools
STEM Discipline: Mathematics
 Description: We created an adaptation to lesson study. Teachers discussed animations made by the research team to get ideas for planning a problem-based lesson. We recorded the teachers’ implementation of the lessons and led video clubs in the reflection step for teachers to pay attention to student thinking. Specifically, we were interested in problems where students could draw on their prior knowledge and experiences of the contexts framing the problems to develop mathematical understanding. Our project used the notion of noticing to propose ways in which teachers can notice the prior knowledge that students bring in the design and implementation of problem-based lessons.
Description: We created an adaptation to lesson study. Teachers discussed animations made by the research team to get ideas for planning a problem-based lesson. We recorded the teachers’ implementation of the lessons and led video clubs in the reflection step for teachers to pay attention to student thinking. Specifically, we were interested in problems where students could draw on their prior knowledge and experiences of the contexts framing the problems to develop mathematical understanding. Our project used the notion of noticing to propose ways in which teachers can notice the prior knowledge that students bring in the design and implementation of problem-based lessons.
Products: We developed 4 geometry problems situated in realistic contexts for high school students to use their prior knowledge. Our publications show examples of ways in which they draw on their prior knowledge during problem-solving. We also developed a set of animations with examples of how teachers can use that prior knowledge during a problem-based lesson and guidance for engaging in a lesson study cycle using the problems as a source. The project website has the problems, the animations, and a list of publications; a total of 13 journal publications (and 1 in-press), 2 book chapters (1 in press), and more than 20 presentations.
COnceptual Model-based Math Intervention Tutor (COMMIT) (NSF #1503451)
PI: Yan Ping Xin | Co-PIs: Yingjie Victor Chen, Signe Kastberg
Target Audience: Second, third, fourth grade students with learning difficulties in mathematics
STEM Discipline: Mathematics
 Description: Integrating best practice from mathematics education and special education through collaborative work including scholars from both fields as well as computer technology, the Purdue University team has created a web-based Conceptual Model-based Math Intervention Tutor (COMMIT) program. The goal of the COMMIT program is to build up mathematics reasoning and problem-solving ability of elementary students with learning difficulties in mathematics (LDM). Rather than focus on superficial story features of the word problem, the COMMIT program emphasizes mathematical model-based problem-solving that is built on nurturing fundamental mathematical ideas that enable students with LDM to make sense of mathematical models at the symbolic level. Model-based learning is one of the foci of theCommon Core mathematical practices (Common Core State Standards Initiative, 2012). Another feature of the COMMIT program is the application of linguistic scaffolding. Through innovative creation and application of “word problem story grammar” (Xin, Wiles, & Lin, 2008), this linguistic scaffolding helps students grasp the key elements that make up the mathematical model for generalized problem-solving. COMMIT can be used as part of the core curriculum or as a supplemental program to address today’s challenging mathematics curriculum standards and diverse student populations in inclusive classrooms.
Description: Integrating best practice from mathematics education and special education through collaborative work including scholars from both fields as well as computer technology, the Purdue University team has created a web-based Conceptual Model-based Math Intervention Tutor (COMMIT) program. The goal of the COMMIT program is to build up mathematics reasoning and problem-solving ability of elementary students with learning difficulties in mathematics (LDM). Rather than focus on superficial story features of the word problem, the COMMIT program emphasizes mathematical model-based problem-solving that is built on nurturing fundamental mathematical ideas that enable students with LDM to make sense of mathematical models at the symbolic level. Model-based learning is one of the foci of theCommon Core mathematical practices (Common Core State Standards Initiative, 2012). Another feature of the COMMIT program is the application of linguistic scaffolding. Through innovative creation and application of “word problem story grammar” (Xin, Wiles, & Lin, 2008), this linguistic scaffolding helps students grasp the key elements that make up the mathematical model for generalized problem-solving. COMMIT can be used as part of the core curriculum or as a supplemental program to address today’s challenging mathematics curriculum standards and diverse student populations in inclusive classrooms.
Current Findings Related to Problem Solving: We conducted a RCT study involving 18 students with LDM to investigate the effects of the web-based computer tutor, COMMIT, on enhancing mathematical word problem-solving performance of students with LDM. Findings from this study indicated that COMMIT, which emphasizes mathematical model-based problem-solving, boosted participants’ performance above and beyond the business-as-usual (BAU) group. That is, although both groups improved their performance from pre- to posttest, the improvement rate of the students in the COMMIT group (effect size [ES]COMPS = 1.88) is much larger than that of the students in the BAU group (ESBAU = 0.98). Using gain scores as the measure, the ES between the two groups was 1.32 favoring the COMPS group. Additionally, the COMMIT group also took the Mathematics Problem Solving subset of the Stanford Achievement Test (SAT-10; Harcourt Assessment, 2004) before and after the COMMIT intervention. Results on SAT scores indicate that five out of nine (56%) participants in the COMPS-A group improved their SAT percentile rank after the intervention.
Key Challenge: One challenge in conducting this type of work is the interdisciplinary nature of the work. The development of educational technologies requires the expertise of a diverse group of scholars who draw from different views of teaching and learning. Creating effective interfaces for learners and teachers demands that project team members develop a negotiated view of teaching and learning that can be drawn upon in the design of instructional activities, the programming of tools, and the implementation of the educational technology. Our engagement in conversations of views of teaching and learning overtime eventually result in a shared view.
Products: Project Website | 2020 STEM for All Video Showcase Entry
National/Internationally Refereed Journal Articles
- Xin, Y. P., Kim, S. J., Lei, Q., Wei, S., Liu, B., Wang, W., Kastberg, S., Chen, Y., Yang, X., Ma, X., Richardson, S. E. (2020). The impact of a conceptual model-based intervention program on math problem-solving performance of at-risk English learners. Reading and Writing Quarterly, 36(2), 104-123. https://www.tandfonline.com/doi/full/10.1080/10573569.2019.1702909
- Xin, Y. P., Park, J., Tzur, R., & Si, L. (2020). The impact of a conceptual model-based mathematics computer tutor on multiplicative reasoning and problem-solving of students with learning disabilities. The Journal of Mathematical Behavior, 58. available online Feb 27, 2020. https://doi.org/10.1016/j.jmathb.2020.100762
- Xin, Y. P. (2019). The effect of a conceptual model-based approach on “additive” word problem solving of elementary students who are struggling in mathematics. ZDM: Mathematics Education, 51(1), 139-150. DOI: 10.1007/s11858-018-1002-9
- Xin, Y. P.,Chiu, M. M., Tzur, R. Ma, X., Park, J., Yang, X. (2019). Discourse-oriented instruction: How does a teacher’s talk affect math problem solving and reasoning of students with Learning disabilities. Learning Disability Quarterly, 43, 43-56 doi.org/10.1177/0731948719858707".
- Xin, Y. P., Tzur, Si, L. Hord, C., Liu, J., Park, J. Y. (2017). An intelligent tutor-assisted math problem-solving intervention program for students with learning difficulties. Learning Disability Quarterly, 40(1), 4-16.
- Xin, Y. P., Liu, J., Jones, S., Tzur, R., SI, L. (2016). A preliminary discourse analysis of constructivist-oriented math instruction for a student with learning disabilities. The Journal of Educational Research, 109(4), 436-447. DOI:10.1080/00220671.2014.979910
- Xin, Y. P. & Hord, C. (2013). Conceptual model-based teaching to facilitate geometry learning of students who struggle in mathematics. Journal of Scholastic Inquiry: Education, 1(1), 147-160.
- Hord, C. & Xin, Y. P. (2013). Intervention research for helping elementary school students with math learning difficulties understand and solve word problems: 1996-2010. Learning Disabilities: A Multidisciplinary Journal, 19(1), 3-17.
- Zhang, D, Xin, Y. P., & Si, L. (2013). Transition from intuitive to advanced strategies in multiplicative reasoning for students with math difficulties. The Journal of Special Education, 47(1), 50-64.
- Xin, Y. P., Si, L., Hord, C., Zhang, D., Cetintas, S., & Park. J. Y. (2012). The effects of computer-assisted instruction in teaching Conceptual Model-Based problem solving. Learning Disabilities: A Multidisciplinary Journal, 18(2), 71-85.
- Xin, Y. P., Zhang, D., Park, J. Y., Tom, K., Whipple, A., & Si, L. (2011). A comparison of two mathematics problem-solving strategies: Facilitate algebra-readiness. The Journal of Educational Research, 104, 381-395.
- Cetintas, S, Si, L., Xin, Y. P., Zhang, D., Park, J. Y. & Tzur, R. (2010). A joint probabilistic classification model of relevant and irrelevant sentences in mathematical word problems. Journal of Educational Data Mining, 2(1), 83-101.
- Cetintas, S., Si, L., Xin, Y. P., and Hord, C. (2010). Automatic detection of off-task behaviors in intelligent tutoring systems with machine learning techniques. IEEE Transactions on Learning Technologies, 3(3), 228-236.
- Xin, Y. P. & Zhang, D. (2009). Exploring a conceptual model-based approach to teaching situated word problems. The Journal of Educational Research, 102(6), 427-441.
- Xin, Y. P. (2008). The effect of schema-based instruction in solving word problems: An emphasis on pre-algebraic conceptualization of multiplicative relations. Journal for Research in Mathematics Education, 39, 526-551.
- Xin, Y. P., Wiles, B., & Lin, Y. (2008). Teaching conceptual model-based word-problem story grammar to enhance mathematics problem solving. The Journal of Special Education, 42, 163-178.
Peer-Reviewed Proceedings
- Kim, S., Kastberg, S. Xin, Y. P. Chen Y. & Wei, S. (2018). Development of the composite unit in additive problem solving of student with mathematics difficulty in a computer based-learning environment. In Hodges, T.E., Roy, G. J., & Tyminski, A. M. (Eds.). (2018). Proceedings of the 40th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (p.1280). Greenville, SC: University of South Carolina & Clemson University.
- Lei, Q., Xin, Y., P., Morita-Mullaney, T., & Tzur, R. (2018). Analyzing a discourse of scaffolds for mathematics instruction for an ELL with learning disabilities. In Hodges, T.E., Roy, G. J., & Tyminski, A. M. (Eds.). (2018). Proceedings of the 40th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 460-467). Greenville, SC: University of South Carolina & Clemson University.
- Wei, S., Xin,Y.P., & Chen,Y. (2020). Visualizing Students' Eye Movement to Understand Their Problem-Solving Process". Accepted by the Proceedings of the 22nd International Conference on Human Computer Interaction, Copenhagen, Denmark.
- Wei, S., Lei, Q., Chen, Y., Xin, Y. P., Kastberg, S., & Kim, S. (2018). Evaluating the effects of highlighting text animations on the attention distribution of students with math learning difficulties. Proceedings of the 2018 American Society for Engineering Education (ASEE) Conference.
- Wei, S., Chen, Y., Xin, Y. P., Kastberg, S. (2018). An exploratory approach to analyzing students’ eye movements when solving math problems. In Hodges, T.E., Roy, G. J., & Tyminski, A. M. (Eds.). (2018). Proceedings of the 40th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1259-1262). Greenville, SC: University of South Carolina & Clemson University.
- Xin, Y. P., Kim; S., Kastberg, S., Chen, Y., Liu, B., Lei, Q., Wang, W., Richardson, S. E., Wei, S. (2018). The effect of a computer-assisted model-based problem-solving program for students with learning difficulties in mathematics. In Hodges, T.E., Roy, G. J., & Tyminski, A. M. (Eds.). (2018). Proceedings of the 40th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp.1267-1270). Greenville, SC: University of South Carolina & Clemson University.
- Xin, Y. P., Kastberg, Si., & V. Chen. (2017). Conceptual Model-based Problem Solving: A response to intervention program for students with LDM. In E. Galindo & J. Newton (Eds.) Proceedings of the 39th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Indianapolis, IN: Hoosier Association of Mathematics Teacher Educators, pp. 326.
- Xin, Y. P., Yang, X., Tzur, R. Park J., Ma. X (2016). PGBM-COMPS math problem-solving program: promote independent problem solving of students with LD. Proceedings of 13th International Congress on Mathematical Education (ICME), Hamburg Germany.
DEAP: Developing and Evaluating Assessments of Problem Solving (NSF #s 1720646, 1720661)
PIs: Jonathan Bostic, Toni Sondergeld | Co-PI: Gabriel Matney
Target Audience: Researchers interested in assessment development and use in STEM contexts; grades 3-8 mathematics teachers and school administrators
STEM Discipline: Mathematics
 Description: If mathematics teachers are expected to engage their students in problem solving during classroom instruction, assessment of students’ problem-solving performance and growth must be conducted using tools that produce meaningful, valid, and reliable outcomes. Based on this premise, DEAP’s main purpose is to develop, pilot, validate, and vertically equate mathematical problem-solving measures for grades 3-5 (PSM 3-5). Creation of these assessments builds on previously established and vertically equated PSMs for grades 6-8 (see Bostic & Sondergeld, 2015, 2018; Bostic et al., 2017). All PSM items are intentionally aligned with the Common Core State Standards for Mathematics (CCSSM) and address problem solving through CCSSM content and practice standards.
Description: If mathematics teachers are expected to engage their students in problem solving during classroom instruction, assessment of students’ problem-solving performance and growth must be conducted using tools that produce meaningful, valid, and reliable outcomes. Based on this premise, DEAP’s main purpose is to develop, pilot, validate, and vertically equate mathematical problem-solving measures for grades 3-5 (PSM 3-5). Creation of these assessments builds on previously established and vertically equated PSMs for grades 6-8 (see Bostic & Sondergeld, 2015, 2018; Bostic et al., 2017). All PSM items are intentionally aligned with the Common Core State Standards for Mathematics (CCSSM) and address problem solving through CCSSM content and practice standards.
Theoretical Framework: All PSM items are problems for students to solve, rather than exercises. For this project, problems are characterized as tasks meeting the following criteria: (a) it is unknown whether a solution exists, (b) a solution pathway is not readily determined, and (c) there exists more than one way to answer the task (Schoenfeld, 2011). PSM tasks are word problems, thus we draw upon a framework from Verschaffel and colleagues (1999) such that the word problems are (a) open, (b) developmentally complex, and (c) realistic tasks for an individual. Open tasks can be solved using multiple developmentally-appropriate strategies. Complex tasks are not readily solvable by a respondent and require productive thinking. Realistic tasks may draw upon real-life experiences, experiential knowledge, and/or believable events. Problems are distinct from exercises, whereas exercises are tasks intended to promote efficiency with a known procedure (Kilpatrick et al., 2001). Further, problem solving goes beyond the type of thinking needed to solve exercises (Mayer & Wittrock, 2006) and occurs when the task is a problem, not an exercise (Schoenfeld, 2011).
Methodology: Once initial items are developed for PSMs, a systematic process is undertaken to collect five types of validity evidence, as suggested in The Standards for Educational and Psychological Testing (AERA et al., 2014): test content, response process, internal structure, relationship to other variables, and consequential. These sources of validity evidence inform continued or discontinued use of an item and whether additional items need to be developed. Test content validity evidence is collected through subject matter experts, including mathematics teachers, mathematics educators, and mathematicians, evaluating item-to-construct alignment through qualitative (logical or empirical) methods (Sireci & Faulkner-Bond, 2014). One-on-one and whole-class think alouds (Bostic et al., 2020) with typical student participants are used to inform response process validity evidence to ensure participant responses align with the test construct (Padilla & Benitez, 2014). For DEAP, internal structure validity evidence is assessed psychometrically using Rasch (1960) methods to explore instrument dimensionality, measurement invariance, and instrument reliability (Rios & Wells, 2014). Relationship to other variables validity evidence uses statistical testing to determine if PSM outcomes are associated with hypothesized variables (Beckman et al., 2005). Finally, consequential validity evidence (or bias) is examined through interviews to see how participants perceived the assessment to have impacted them (Bostic & Sondergeld, 2015) and through Rasch differential item functioning (DIF) analyses. Taken collectively, this evidence fuels the validity argument, which communicates how PSM users know score interpretations are appropriately grounded in sound claims and validity evidence.
Current Findings Related to Problem Solving: Initial findings show that our team has successfully developed three problem-solving measures (PSM 3-5) that assess students’ abilities to solve CCSSM grade-level aligned problems. Each assessment has been explored rigorously through multiple validation studies to produce meaningful measures and score interpretations for researchers and schools. To date, anchor items used for linking assessments to each other have been initially tested and overall demonstrate acceptable for continued use. In our final year, we will test the vertical equating linking to ensure our operationalized construct of problem-solving ability from grades 3 to 8 has been appropriately measured in the anticipated manner.
Key Challenge: Rigorous assessment development and validation is time intensive as it takes multiple cycles of creating and revising. Additionally, this work takes expertise from many different domains – subject matter experts, psychometricians, and school partners. It has taken our team many years of working together with diverse districts to construct a suitable test development process to conduct this type of work effectively and efficiently.
Products:
- Bostic, J., Matney, G., Sondergeld, T., & Stone, G. (2020, April). Validation as design-based research: Implications for practice and theory. Paper presented at annual meeting of the annual meeting of the American Education Research Association. San Francisco, CA.
- Bostic, J., Matney, G., Sondergeld, T., & Stone, G. (2020, April). Developing a series of problem-solving measures for elementary students. Paper presented at annual meeting of the annual meeting of the American Education Research Association. San Francisco, CA.
- Bostic, J., Matney, G., Sondergeld, T., & Stone, G. (2020, March). Measuring what we intend: A validation argument for the grade 5 problem-solving measure (PSM5). Validation: A Burgeoning Methodology for Mathematics Education Scholarship. In J. Cribbs & H. Marchionda (Eds.), Proceedings of the 47th Annual Meeting of the Research Council on Mathematics Learning (pp. 59-66). Las Vegas, NV.
- Bostic, J., Matney, G., Sondergeld, T., & Stone, G. (2019, July). Developing a problem-solving measure for grade 4. In M. Graven, H. Venkat, A. Essien, & P. Vale (Eds.), Proceedings of the 43rd Meeting of the International Group for the Psychology of Mathematics Education (Vol. 4, p 4-104). Pretoria, South Africa. https://www.up.ac.za/media/shared/705/pme43/Proceedings/PME43Volume-4-proceedings-oc_pp.pdf
- Bostic, J.(2019, October). We can do better! Intersection Points, 44(6), p. 3-4.
- Bostic, J., Matney, G., Sondergeld, T., & Stone, G. (2019, February). Validation: A Burgeoning Methodology for Mathematics Education Scholarship. In A. Sanogo & J. Cribbs (Eds.), Proceedings of the 46th Annual Meeting of the Research Council on Mathematics Learning (pp. 43-50). Charlotte, NC.
- Bostic, J.,Matney, G., Sondergeld, T., & Stone, G. (2018, November). Content validity evidence for new problem-solving measures (PSM3, PSM4, and PSM5). In T. Hodges, G. Roy, & A. Tyminski (Eds.), Proceedings for the 40h Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1641). Greenville, SC.
- Sondergeld, T. A. (2020). Shifting sights on STEM education instrumentation development: The importance of moving validity evidence to the forefront rather than a footnote. School Science and Mathematics Journal. https://onlinelibrary.wiley.com/doi/abs/10.1111/ssm.12410?af=R
- Sondergeld, T., Stone, G., Kruse, L., Bostic, J., & Matney, G. (2020, April). Evaluating Dichotomous and Partial-Credit Scoring within a Constructed-Response Assessment: Is More Information Always Psychometrically Better?Paper presented at annual meeting of the annual meeting of the American Education Research Association. San Francisco, CA.
- Sondergeld, T., Stone, G., Bostic, J., & Matney, G., (2019, July). Validity in a different context: Exploring relations to other variables evidence. In M. Graven, H. Venkat, A. Essien, & P. Vale (Eds.), Proceedings of the 43rd Meeting of the International Group for the Psychology of Mathematics Education (Vol. 4, p. 4-104). Pretoria, South Africa. https://www.up.ac.za/media/shared/705/pme43/Proceedings/PME43Volume-4-proceedings-oc_pp.pdf
- Stone, G. E., Sondergeld, T. A., Bostic, J., & Matney, G. (2019, July). Validity in a different context: Exploring relationship to other variables validity evidence. In M. Graven, H. Venkat, A. Essien, & P. Vale (Eds.), Proceedings of the 43rd Meeting of the International Group for the Psychology of Mathematics Education (Vol. 4, p. 4-104). Pretoria, South Africa. https://www.up.ac.za/media/shared/705/pme43/Proceedings/PME43Volume-4-proceedings-oc_pp.pdf
Ed+gineering: An Interdisciplinary Partnership Integrating Engineering into Elementary Teacher Preparation Programs (NSF #1908743)
PI: Jennifer Kidd | Co-PIs: Kristie Gutierrez, Krishnanand Kaipa, Pilar Pazos-Lago, Stacie Ringleb
Target Audience: Our project partners undergraduate education and engineering students to teach engineering lessons to 4th and 5th graders.
STEM Discipline: Engineering
 Description: Engineering and elementary education share complementary challenges. New standards require elementary teachers to teach engineering. Most teachers however, have no training in engineering, and feel unprepared to do so. Engineers are increasingly asked to tackle multidisciplinary problems, often without experience collaborating in such contexts. Ed+gineering addresses these challenges through a partnership between Old Dominion University's Colleges of Education and Engineering. The project partners preservice teachers (PSTs) with engineering students to collaboratively plan and teach engineering lessons to elementary school students. Working in small cross-disciplinary teams in three paired classes, the college students engage in engineering design challenges and learn about culturally responsive pedagogy. They then address a complex problem: Develop a lesson for 4th/5th graders that will help broaden participation in engineering. The undergraduates must devise and teach an engineering design challenge that connects with the children’s interests and backgrounds.
Description: Engineering and elementary education share complementary challenges. New standards require elementary teachers to teach engineering. Most teachers however, have no training in engineering, and feel unprepared to do so. Engineers are increasingly asked to tackle multidisciplinary problems, often without experience collaborating in such contexts. Ed+gineering addresses these challenges through a partnership between Old Dominion University's Colleges of Education and Engineering. The project partners preservice teachers (PSTs) with engineering students to collaboratively plan and teach engineering lessons to elementary school students. Working in small cross-disciplinary teams in three paired classes, the college students engage in engineering design challenges and learn about culturally responsive pedagogy. They then address a complex problem: Develop a lesson for 4th/5th graders that will help broaden participation in engineering. The undergraduates must devise and teach an engineering design challenge that connects with the children’s interests and backgrounds.
Ed+gineering’s goal is to increase PSTs’ engineering confidence and engineering students’ ability to communicate effectively in interdisciplinary contexts. Teaching engineering lessons in a supported context helps increase PSTs’ self-efficacy and intention to teach engineering. Engineering students who seek out and value the contributions of non-technical peers are well positioned to address complex global challenges.
Products: Coming Soon! Project Website
Project Videos
- 2020 STEM for All Video Showcase Entry
- Teaching robotics while quarantined: A profile of one team’s journey (Ed+gineeringODU Spring 2020)
- Pilot-projects that lead to the DRK12 Ed+gineering Project
ASEE 2020 Conference Presentations
- What do Undergraduate Engineering Students and Pre-service Teachers Learn by Collaborating and Teaching Engineering and Coding Through Robotics?
- The First Year of an Undergraduate Service Learning Partnership to Enhance Engineering Education and Elementary Pre-Service Teacher Education
- Enhancing Teamwork Skills Through an Engineering Service-learning Collaboration
- Partnering Undergraduate Engineering Students with Preservice Teachers to Design and Teach an Elementary Engineering Lesson Through Ed+gineering
FLECKS: Fostering Collaborative Computer Science Learning with Intelligent Virtual Companions for Upper Elementary Students (NSF #s 1721000, 1721160)
PIs: Kristy Boyer, Eric Wiebe | Co-PI: Collin Lynch
Target Audience: Upper elementary (Grades 4-5) students, especially populations that historically have been underrepresented in Computer Science
STEM Discipline: Computer Science
 Description: The FLECKS project will create a collaborative computer science learning environment for upper elementary school classrooms. FLECKS addresses the pressing need for young students to develop fundamental computer science competencies and collaboration practices. One of the central tenets of modern computer science is that it is a collaborative discipline, yet many students have not received direct support or appropriate modeling as to how to collaborate effectively while problem-solving. Our goal is to develop an adaptive learning environment which utilizes interactive agents to help support CS learning and productive collaboration. Our work to date has contributed important understandings of how young students collaboratively problem-solve as they program. These findings have guided explorations of differing paired programming configurations, and how teachers can directly support productive collaboration. Students have also participated in the design of avatars and the learning environment. Informed by these findings, we expect our learning environment to provide a new approach to supporting collaborative computational learning in the classroom.
Description: The FLECKS project will create a collaborative computer science learning environment for upper elementary school classrooms. FLECKS addresses the pressing need for young students to develop fundamental computer science competencies and collaboration practices. One of the central tenets of modern computer science is that it is a collaborative discipline, yet many students have not received direct support or appropriate modeling as to how to collaborate effectively while problem-solving. Our goal is to develop an adaptive learning environment which utilizes interactive agents to help support CS learning and productive collaboration. Our work to date has contributed important understandings of how young students collaboratively problem-solve as they program. These findings have guided explorations of differing paired programming configurations, and how teachers can directly support productive collaboration. Students have also participated in the design of avatars and the learning environment. Informed by these findings, we expect our learning environment to provide a new approach to supporting collaborative computational learning in the classroom.
Theoretical Framework: The theoretical work of Mercer and colleagues (1999; 2002; 2004) has informed both our analysis of collaborative work and the goals for more productive collaboration. In addition, we are also interested in how dyads of students regulate their collaboration. This theoretical lens is informed by the work of noted scholars in the field (Hadwin, Wozney, & Pontin, 2005; Janssen, Erkens, Kirschner, & Kanselaar, 2010; and Kumpulainen & Mutanen, 1999).
Methodology: The primary approach to analyzing student discourse has been qualitative analysis of video and audio recordings of student work, guided by rubrics designed through the lens of the above-mentioned theoretical frameworks. In addition, we make extensive use of participatory design techniques in the development of our prototype learning environments. More recently, we have also been utilizing Epistemic Network Analysis (ENA; Shaffer, Collier & Ruis, 2016) to further unpack students’ discursive practices.
Current Findings Related to Problem Solving: Productive collaborative problem solving does not just happen, especially with younger students. Efficacious practices have to be modeled and supported by teachers and intelligent systems. We have learned that interpersonal dynamics will often lead students away from productive problem-solving and into unproductive conflict if not properly supported. Similarly, students need to be taught how to employ questioning techniques that move beyond low level questioning, where they are spurring deeper thinking on the part of their partner as they explain and defend their strategies and solutions.
Key Challenge: One of our challenges is the development of activities and design of a learning environment that serves and supports a diverse audience of students. In addition, elementary teachers have historically not taught computer science or collaborative problem solving in technology-rich environments. We have had to devote effort to properly supporting teachers and seeking feedback from a broad range of students through our design and development process.
Products:
- Tsan, J., Vandenberg, J., Fu, X., Wilkinson, J., Boulden, D., Wiebe, E., Lynch, C., & Boyer, K. E. (June, 2019). Conflicts and collaboration: A study of upper elementary students solving computer science problems. International Conference on Computer Supported Collaborative Learning (CSCL 2019). Lyon, France.
- Tsan, J., Vandenberg, J., Fu, X., Wilkinson, J., Boulden, D., Boyer, K. E., ... & Wiebe, E. (February, 2019). An investigation of conflicts between upper-elementary pair programmers. Proceedings of the 50th ACM Technical Symposium on Computer Science Education (pp. 1264-1264). ACM.
- Tsan, J., Vandenberg, J., Zakaria, Z., Wiggins, J. B., Webber, A. R., Bradbury, A., Lynch, C., Wiebe, E., Boyer, K. E., (2020, March) A comparison of two pair programming configurations for upper elementary students. Proceedings of the 51st ACM Technical Symposium on Computer Science Education (SIGCSE ’20), Portland, OR (pp. 346-352).
- Vandenberg, J., Tsan, J., Boulden, D. C., Zakaria, Z., Lynch, C., Boyer, K. E., & Wiebe, E. (2020). Elementary students' understanding of CS terms. ACM Transactions on Computing Education (TOCE), 20(3). https://dl.acm.org/doi/pdf/10.1145/3386364
- Vandenberg, J., Tsan, J., Zakaria, Z., Boulden, D. C., Boyer, K. E., Lynch, C., & Wiebe, E. N. (2020, April). Elementary learners’ regulation in computer-supported collaborative learning environments. Paper accepted for presentation at the annual meeting of the American Educational Research Association (AERA), San Francisco, CA.
- Wiggins, J., Wilkinson, J., Lynch, C., Wiebe, E., & Boyer, K. E. (June, 2019). From doodles to designs: Participatory edagogical agent design with elementary students. Proceedings of the 18th ACM International Conference on Interaction Design and Children (IDC 2019) (pp. 642-647). ACM. doi: 10.1145/3311927.3325321
- Zakaria. Z., Boulden. D. C., Vandenberg, J., Tsan, J., Lynch, C. Boyer, K. E. & Wiebe, E. N. (April, 2019). Elementary students’ collaborative practices in side-by-side programming. AERA Annual Meeting, Toronto, CA.
- Zakaria, Z., Vandenberg, J., Boulden, D. C., Tsan, J., Boyer, K. E., Lynch, C., & Wiebe, E. N. (2020, April). Feedback to improve collaboration in pair programming. Paper accepted for presentation at the annual meeting of the American Educational Research Association (AERA), San Francisco, CA.
- Zakaria, Z., Wiebe, E., Boulden, D., Tsan, J., Vandenberg, J., Lynch, C. & Boyer, K. (June, 2019). Collaborative talk across two pair-programming configurations. International Conference on Computer Supported Collaborative Learning (CSCL 2019). Lyon, France.
Improving Grades 6-8 Students' Mathematics Achievement in Modeling and Problem Solving through Effective Sequencing of Instructional Practices (NSF #1907840)
PI: Joe Champion | Co-PIs: Michele Carney, Samuel Coskey, Ya Mo, Keith Thiede
Target Audience: Grades 6-8 students
STEM Discipline: Mathematics
Description: Researching Order of Teaching (ROOT) is a teacher-researcher alliance to investigate classroom interventions for improving Grades 6-8 students’ mathematics achievement in the content area of modeling and problem solving. Leveraging ongoing partnerships with 35 regional schools, many rural with low enrollment, the project engages 100 teachers in the co-production of professional knowledge, designing and implementing classroom studies of instructional practices supporting achievement in a domain integral to the shifting landscape of STEM education. Collaborative professional development supports implementation, while rigorous research methods provide findings to extend theory of effective mathematics teaching emphasizing Explicit Attention to Concepts (EAC) and Students’ Opportunities to Struggle (SOS) (Hiebert & Grouws, 2007). The research design features cluster crossover trials, a popular method for evaluating interventions in clinical medicine, adapted for assessment of instructional effects in middle grades, and analyzed using a hierarchical linear model for student achievement.
Theoretical Framework: ROOT aims to adopt and extend features of effective mathematics instruction as outlined by Hiebert and Grouws (2007). The Explicit Attention to Concepts (EAC) and Students’ Opportunities to Struggle (SOS) conceptual framework was successfully used by Stein and colleagues (2017) for large-scale classroom teacher research, and our project has been heavily invested in extending Stein’s work through a combination of video analysis, surveys, and student achievement data.
Key Challenge: ROOT addresses the key challenge of conducting classroom intervention research that both offers support and choice for teachers to innovate in their local context and generates transferable research evidence about how instructional strategies can improve student learning.
Product: Project Website | PD Modules One, Two, Three | EAC & SOS Guide
Mathematical and Computational Methods for Planning a Sustainable Future (PS-Future) (NSF #1503414)
PI: Margaret Cozzens | Co-PIs: Tamra Carpenter, Rebecca Jordan
Target Audience: High school
STEM Disciplines: Mathematics, Environmental Science, Biology, Computing, Social Sciences
 Description: PS-Future has developed instructional modules that bring sustainability topics into classrooms in a way that emphasizes the methods and tools of mathematics and computing and illustrates their role in planning for sustainability. Through the modules, students learn foundational and emerging concepts in mathematical and computational sciences set in the context of sustainability issues involving physical, biological, environmental, and social sciences. Students develop an increasingly sophisticated understanding of the ways that these disciplines interact through inquiries driven by real problems such as combating invasive species, understanding environmental threats, managing water resources, interpreting weather data, and simply living greener. By exploring real-life problems, students develop an appreciation for the wide applicability of the mathematical and computational sciences, while also becoming immersed in some of the most pressing problems facing the global community.
Description: PS-Future has developed instructional modules that bring sustainability topics into classrooms in a way that emphasizes the methods and tools of mathematics and computing and illustrates their role in planning for sustainability. Through the modules, students learn foundational and emerging concepts in mathematical and computational sciences set in the context of sustainability issues involving physical, biological, environmental, and social sciences. Students develop an increasingly sophisticated understanding of the ways that these disciplines interact through inquiries driven by real problems such as combating invasive species, understanding environmental threats, managing water resources, interpreting weather data, and simply living greener. By exploring real-life problems, students develop an appreciation for the wide applicability of the mathematical and computational sciences, while also becoming immersed in some of the most pressing problems facing the global community.
Project research and evaluation studies investigated and validated our belief that short (roughly one week) modules can positively impact students’: 1) engagement in mathematics and computing by immersion in sustainability topics of personal relevance; 2) confidence in using cross-cutting skills in mathematical and computational methods for scientific inquiry; and 3) learning of the STEM practices and modes of inquiry necessary to become the next generation of interdisciplinary problem solvers.
Theoretical Framework & Methodology: Given the increased demand for inter- and cross-disciplinary thinking, especially in environmental and sustainability related fields, special attention needs to be given to the means by which these complex environmental problems are understood. We feel that thinking within complex systems is essential for learners to grasp the non-linear and dynamic nature of real world problems and have focused our PS Futures learning modules on the quantitative reasoning and operations associated with sustainability related problems. Our work is nested in theory that suggests that learning is mediated by the tools and outcomes in an activity system surrounding the learners and that learners need to collaboratively attend to abstractions that can help encourage learning transfer (e.g., Palincsar 1998; Bransford et al. 1999). The tools and outcomes in our modules integrate social and scientific concepts embedded in mathematical operations that students encounter in their math and environmental science courses. We use mental models made visible through a specific conceptual representation that helps the learners to tie together the multiple ideas encountered in the modules. Because models often include a small number of semantic representations, individuals coming from different backgrounds, classrooms, and engaging with different task structures, once familiar with model terms, can communicate their ideas in a standardized space that can be compared across contexts.
Current Findings Related to Problem Solving: We were able to code data from 84 pre-module and 147 post-module models in which learners were asked to tie together ideas and transfer knowledge to a novel context. In this way, these learners can describe on a system level the mathematical strategies necessary to understand the environmental problem posed. From these models a number of trends emerged. First, and not surprisingly, the models were more accurate following instruction. Second, the post-module models tended to represent more causal agents, which suggests an increased understanding of how specific phenomena are driven by underlying mechanisms versus specific parts. In this way, we argue that as learners encounter novel spaces where similar thinking strategies are warranted, they are more likely to implement their more accurate mathematical practices. To support this contention, we found that when students represented greater mechanism they tended to do so at a more abstract scale, which tend to be more applicable across environments. While at this point only a speculation, there is enough evidence to suggest deeper investigation would be enlightening.
Key Challenges: As we were finishing publication of the modules, we discovered that the Cornell Ornithology Center was no longer supporting the “Yardmap” software they had developed, and by January 31, 2020, they had pulled it entirely from their website. One of the modules, called Life on the Edge, made extensive use of the software by students in designing suitable habitats. This section had to be rewritten and a new methodology found for developing and representing animal habitats. Fortunately, we were able to use Google Earth to accomplish all of tasks required. Google Earth is available to students through Google Classroom or independently. This work was completed in early June, completing the module development.
A typical challenge for this type of work is that of implementing a complex pre-post test project evaluation that involves models versus finite-scope types of questionnaires. That is to say, learners have the open space to model whatever aspect of the novel system, which can result in numerous possibilities that may reflect classroom-specific detail versus across-classroom ideas.
Doing this type of work, requires that the classroom instructors invest similar amounts of time and intellectual energy to the task which is not always feasible given the incredibly dynamic classroom space.
Products: Instructional Modules | Project Website | 2018 STEM for All Video Showcase Entry
Mathematical Learning via Architectural Design and Modeling Using E-Rebuild (NSF #1720533)
PI: Fengfeng Ke | Co-PIs: Russell Almond, Kathleen Clark, Gordon Erlebacher, Valerie Shute
Target Audience: Middle school students
STEM Disciplines: Mathematics
 Description: This project will explore the learning of mathematical problem solving through architectural tasks in an online simulation game, E-Rebuild. There is a need to connect mathematics to real world contexts and problems. In the game-based architectural simulation, students will be able to complete tasks such as building and constructing structures while using mathematics and problem solving. This learning platform will be flexible so teachers can customize tasks for their students. The project will explore how students learn mathematical problem solving during architectural structure building in E-Rebuild and how the game-based learning platform can be included in middle school mathematics learning. The project will also examine how to collect data about students' learning from the data generated as they play the game.
Description: This project will explore the learning of mathematical problem solving through architectural tasks in an online simulation game, E-Rebuild. There is a need to connect mathematics to real world contexts and problems. In the game-based architectural simulation, students will be able to complete tasks such as building and constructing structures while using mathematics and problem solving. This learning platform will be flexible so teachers can customize tasks for their students. The project will explore how students learn mathematical problem solving during architectural structure building in E-Rebuild and how the game-based learning platform can be included in middle school mathematics learning. The project will also examine how to collect data about students' learning from the data generated as they play the game.
Theoretical Framework: Realistic mathematics education, learning through making and design, constructionism, and learning with multiple representations.
Methodology: The project uses a design-based research approach to gather data from students and teachers that will inform the design of the learning environment. The qualitative and quantitative data will also be used to understand what students are learning as they play the game and how teachers are interacting with their students.
Current Findings Related to Problem Solving: The initial findings of a recent mixed-method infield study indicate a positive effect and an advantage of using E-Rebuild in the classroom, in comparison with a business-as-usual control group, on the math problem-solving test performance of middle school students. There was a significant improvement with a large effect size from pretest to posttest by the E-Rebuild participants in the math problem-solving test performance. Controlling for the pretest performance, the E-Rebuild group significantly outperformed the control group in the post-treatment math problem-solving test with a medium-large effect size. The qualitative behavior analysis of participants’ gameplay processes also indicated a trend of increased engagement in mathematical problem-solving actions and the development of mindfulness with positive attitudes toward mathematical reasoning and conception.
Products: E-Rebuild Game, Tutorial, & Demos
Proportions Playground (NSF #1621290)
PI: Chandra Orrill
Target Audience: Middle school teachers
STEM Disciplines: Mathematics
 Description: This is a proof of concept project focused on helping to improve teachers’ understanding of proportions. We use dynamic environments, that we call toys, to let teachers explore situations that have been designed to encourage playful conversation. We pose questions that challenge common understandings and engage the teachers in wondering about the situations for themselves. These might include asking which of three dynamic situations is proportional or it might engage in asking them to think about the relationship between similarity and proportions. Our focus has been on three big ideas related to proportions: quantities, covariation, and constant. We are learning that constant is particularly tricky because it can be used to describe many different aspects of mathematical relationships. This makes it a rich concept for digging into in our environment.
Description: This is a proof of concept project focused on helping to improve teachers’ understanding of proportions. We use dynamic environments, that we call toys, to let teachers explore situations that have been designed to encourage playful conversation. We pose questions that challenge common understandings and engage the teachers in wondering about the situations for themselves. These might include asking which of three dynamic situations is proportional or it might engage in asking them to think about the relationship between similarity and proportions. Our focus has been on three big ideas related to proportions: quantities, covariation, and constant. We are learning that constant is particularly tricky because it can be used to describe many different aspects of mathematical relationships. This makes it a rich concept for digging into in our environment.
Theoretical Framework: Our work is grounded in two frameworks. The first is Knowledge in Pieces (from diSessa) which allows us a lens to think about how adults understand proportional relationships. While teachers may have a wide range of understandings, those understandings may not be interconnected in ways that support problem solving or the teachers may be missing key knowledge resources. The items we’ve developed attempt to push on making connections between independent knowledge resources, thus deepening teachers’ knowledge bases.
Our other framework is playing with math. This means engaging in problem solving in a way that relies on making and testing conjectures and math arguments that can be reasoned about, tested, illustrated, and explained through the use of dynamic environments. This necessarily occurs in a safe space built on discussion driven by challenges, explorations, and mysteries that are perceived to be worthwhile to engage in and to discuss. Worthwhile tasks are those that are relevant to classroom teaching, allow argument, often feature ambiguity (because that’s where argument can happen), and are open middle and/or open ended.
Methodology: Because this is an exploratory project, we have been using traditional qualitative methods relying primarily on videotaping professional development sessions.
Current Findings Related to Problem Solving: Two critical findings have emerged. First, the teachers love this approach. They rate the experiences very highly, report high engagement, and leave the PD smiling. Teachers want to be challenged, and this approach challenges them. Second, tasks need to be ambiguous to generate the playful exploration necessary to engage in this learning. This is very different from traditional views in which math problems are made as precise as possible. In our conversations, we explicitly discuss the need for precision by building from the perturbation that emerged from the ambiguity.
Products: Proportions Playground Toys | Proportions Playground Tasks
Science and Engineering Education for Infrastructure Transformation (NSF #1721054)
PI: Charles Xie | Co-PIs: Sherry Hsi, Senay Purzer, Pankaj Sharma
Target Audience: Grades 8-12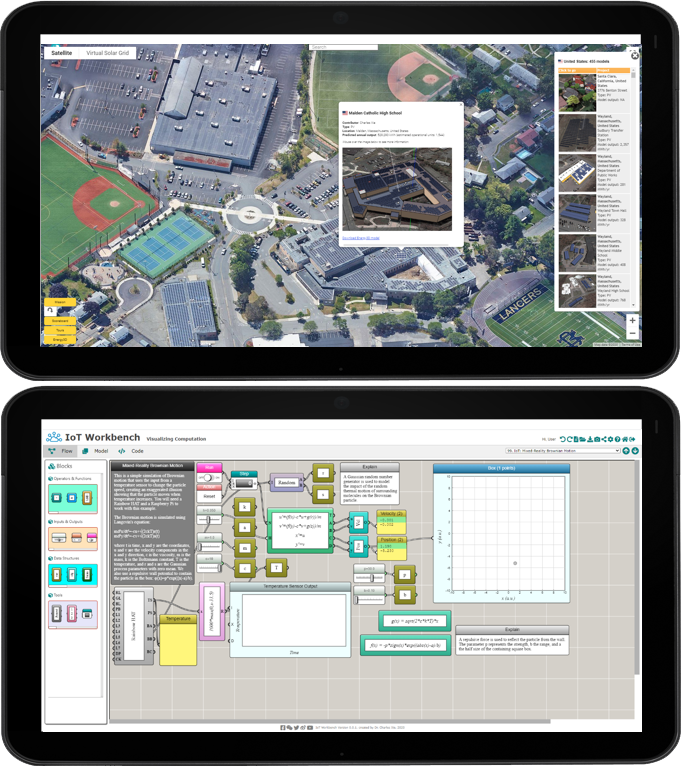
STEM Disciplines: Science, engineering, and computer science
Description: Future sustainable and resilient infrastructure will be powered by renewable energy, be able to respond intelligently to changes in the environment, and support smart and connected communities. The transformation of our infrastructure calls for millions of problem solvers that our education system must cultivate. One way to fill the gap is to build cyberlearning infrastructures that enable students to learn how to solve those problems in the classroom with STEM. This project has developed two such programs, the Virtual Solar Grid and the IoT Workbench. These programs create rich problem-solving activities with sound pedagogies at the intersection of science, engineering, and computation and in the context of solar power engineering and cyber-physical systems. In the past year, we conducted research with 132 high school students and 52 middle school students with highly diverse socioeconomic backgrounds. The results show that students improve their science understanding while acquiring problem-solving abilities such as claim-evidence-reasoning, engineering design, and computational modeling. One of the teachers spoke highly of the solar energy project. “This is the first time of the year that all 16 pairs of eyes paid attention with invested attitudes,” referring to one of her classes that was relatively underperforming.
Products: Virtual Solar Grid | IoT Workbench
Systemic Transformation of Inquiry Learning Environments for STEM (NSF #2010530)
PI: Ellen Meier | Co-PI: Bryan Keller
Target Audience: Grades 3-8, Urban Schools
STEM Discipline: Transdisciplinary STEM; STEM as a meta-discipline; cross-cutting concepts in STEM, which can involve other disciplines beyond science, technology, engineering, and mathematics.
 Description: Many schools across the country are adopting STEM-minded visions for teaching and learning. But what does this really mean for our classrooms? And better yet, how are we supporting teachers in reimagining learning opportunities for STEM? The Systemic Transformation of Inquiry Learning Environments initiative creates a model for instructional change in schools -- one that promotes a meta-approach (or “transdisciplinary” approach) to the disciplines, and which centers the change work on intensive and sustained professional learning for teachers and leaders.
Description: Many schools across the country are adopting STEM-minded visions for teaching and learning. But what does this really mean for our classrooms? And better yet, how are we supporting teachers in reimagining learning opportunities for STEM? The Systemic Transformation of Inquiry Learning Environments initiative creates a model for instructional change in schools -- one that promotes a meta-approach (or “transdisciplinary” approach) to the disciplines, and which centers the change work on intensive and sustained professional learning for teachers and leaders.
With the NSF funding, the project team will study the utility and feasibility of the model in an effort to streamline the approach and to create broader access to high-quality professional learning. Over the course of the project, Grades 3-8 teachers from twenty-five schools in New York City and New Haven, CT will participate in a multi-year online workshop and coaching series to design and implement rigorous and culturally relevant learning experiences focused on cross-cutting concepts across the STEM disciplines. Complementary work with school-based administrators and instructional coaches will support leaders in strategically supporting the change process.
Products: The systemic work leverages the Innovating Instruction approach to professional learning developed by the Center for Technology and School Change at Teachers College, Columbia University. A publically available version is available on the Center’s website.
Zoombinis: The Implementation Research Study of a Computational Thinking Game for Upper Elementary and Middle School Learners (NSF #1502882)
PI: Jodi Asbell-Clarke | Co-PIs: Teon Edwards, Elizabeth Rowe
Target Audience: National, Grades 3-8; Sub-study on students with IEPs or 504s for neurodiversity
Discipline/Focus: Computational Thinking
 Description: Zoombinis is a popular, award-winning, learning game designed by learning scientists in the 1990s to engage learners 8 to adult in computational problem-solving (TERC, 2019). Zoombinis consists of a series of 12 puzzles, each with 4 levels of complexity, in which players lead packs of Zoombinis characters to their safety in Zoombiniville. Each Zoombini has one of five different types of hair, eyes, nose, and feet. Puzzles require sorting, matching, and sequencing of the Zoombinis by their specific attributes. The attributes of the Zoombinis, and associated rules of each puzzle, change with each new round of play so that players must find methods of solving the problems, not just “the right answer.” Other puzzles in the game apply similar logic and CT practices in different contexts such as identifying the exact combination of pizza toppings to satisfy hungry, but picky, trolls.
Description: Zoombinis is a popular, award-winning, learning game designed by learning scientists in the 1990s to engage learners 8 to adult in computational problem-solving (TERC, 2019). Zoombinis consists of a series of 12 puzzles, each with 4 levels of complexity, in which players lead packs of Zoombinis characters to their safety in Zoombiniville. Each Zoombini has one of five different types of hair, eyes, nose, and feet. Puzzles require sorting, matching, and sequencing of the Zoombinis by their specific attributes. The attributes of the Zoombinis, and associated rules of each puzzle, change with each new round of play so that players must find methods of solving the problems, not just “the right answer.” Other puzzles in the game apply similar logic and CT practices in different contexts such as identifying the exact combination of pizza toppings to satisfy hungry, but picky, trolls.
Zoombinis engages learners in problem-solving practices such as Problem Decomposition, Pattern Recognition, Abstraction, and Algorithm Design. We provide “bridge activities” that helps teachers connect the implicit CT problem-solving practices in the game to explicit classroom problem-solving in other subjects such as science and math.
We studied how teachers use the learning game, Zoombinis, to solve problems using Computational Thinking (CT) practices. While students in grades 3-8 solve fun logic puzzles in the game, teachers connect those practices to problem-solving in STEM and everyday activities.
Theoretical Framework: We draw from theory that considers CT as a specific form of problem-solving to study problem solving in the game Zoombinis. Our research goal was to examine how students build CT practices such as problem decomposition, pattern recognition, abstraction, and algorithm design within the context of the increasingly complex logic puzzles in the game.
We also use theory from game-based learning where students build implicit skills and knowledge through engaged problem-solving. This framework differentiates between explicit knowledge, what wecan express, from implicit knowing, which is what we are able to do. Implicit knowledge is, by definition, largely unexpressed by the learner yet is considered foundational to all knowledge. Explicit knowledge is what educators typically attempt to measure in learning assessments. Games present a rich opportunity to support and measure implicit learning because players are often immersed in problem-solving situations where they experiment with the mechanics to understand the rule system, using trial and error with helpful feedback and rewards for motivation and sustain engagement.
We built educational data mining models as a form of embedded implicit assessments, assessments that could measure CT practices using the game log data generated by students’ gameplay. One component of our research study was to examine the validity of these detectors as assessments of students’ CT. Another component of the research was to examine the relationship between students’ activity in the game, teachers’ activity in the class, and the outcomes of students’ CT practices. Our previous research has shown that teachers are key to bridging implicit game-based learning to explicit classroom learning, so we provided teachers with bridging activities and support while they implemented the game in their classes.
Methodolgy: We used a combination of research methods, including educational data mining on game data logs, cluster analysis on teacher logs of classroom activity, and multilevel modeling, to determine the impact of the duration and nature of student gameplay, as well as the extent and nature of classroom activity, on student CT practices.
To develop and validate implicit learning assessments using Zoombinis log data, we designed automated detectors of CT practices within Zoombinis game play. We collected video and screencapture along with data logs from a wide variety of Zoombinis players. After extensive observations and human-labelling of the data, we build educational data mining (EDM) modes to detect those strategies automatically in student gameplay. These automated detectors provide real-time assessment of CT practices students build implicitly within the game.
To validate the detectors as measures of CT, we correlated the detectors with external measures of students’ CT practices. Most CT practice detectors were significantly correlated with these external measures.
To serve as external pre- and post-assessments of CT, the authors worked with a game-based learning company to design Interactive Assessments of CT (IACT)—a set of online, non-coding, non-textual logic puzzles to assess CT practices in upper elementary and middle school.
Current Findings Related to Problem Solving: Automated detectors of gameplay CT practices built for this research were significant predictors of external post-assessment scores, and thus show promise as implicit assessments of CT practices within gameplay.
Students with high duration of gameplay and high gameplay CT practices scored highest on external post-assessment of CT practices, when accounting for pre-assessment scores. This research suggests that Zoombinis is an effective CT learning tool and CT assessment tool for elementary- and middle-school students.
In a small sub-study of classes where we were able to collect students’ IEP status, we found that when teachers used a combination of Zoombinis and classroom bridging activities the outcomes of students with IEP status are comparable to their peers.
Key Challenge: Our biggest challenge was the lack of available external assessments in CT that met the diverse needs of our target audience. We designed our own assessments because we could not find established instruments that did not rely on significant text or coding, which may have been a barrier for some students. In a larger study using an augmented sample, we found moderate evidence of concurrent validity and strong evidence of test-retest reliability for IACT, so we used these for outcome measures in our studies. The research findings would be stronger with a more psychometrically-validated external assessment instrument that also accessible to a broad audience.
Products: Zoombinis Game | Zoombinis Apps (Apple Store, Google Play)
Citations
- Asbell-Clarke, J., Rowe, E., Almeda, V., Edwards, T., Bardar, E., Gasca, S., Baker, R.S., & Scruggs, R. (under review). The Development of Students’ Computational Thinking Practices in Elementary- and Middle-School Classes using the Learning Game, Zoombinis.
- Asbell-Clarke, J. ,Rowe, E. , Almeda, V., Gasca, S. , Edwards, T. , Bardar, E. ,Shute, V. , and Ventura, M. (under review). Interactive Assessments of CT (IACT): Digital Interactive Logic Puzzles to Assess Computational Thinking in Grades 3–8.
- Asbell-Clarke, J., Rowe, E. , Almeda, V., Edwards, T. , Bardar, E. (under review). Bridging the Gap: Using the Computational Thinking Game, Zoombinis, to Support Neurodiverse Learners.
- Rowe, E., Asbell-Clarke, J., & Almeda, M. Scruggs, R., Baker, R.S., Bardar,E. & Gasca, S. (under review) Assessing Implicit Computational Thinking in Zoombinis Puzzle Gameplay. Submitted to a special issue of Computers & Human Behavior on Learning Analytics and Assessment.
- Almeda, M., Rowe, E., Asbell-Clarke, J., Baker, R., Scruggs, R., Bardar, E., & Gasca, S. (2019, October). Modeling Implicit Computational Thinking in Zoombinis Mudball Wall Gameplay. Paper submitted to the Technology, Mind, and Society conference, October, Washington D.C.
- Rowe, E., Asbell-Clarke, J., Almeda, M., Bardar, E., Baker, R. S., & Scruggs, R., (2019). Advancing Research in Game-Based Learning Assessment: Tools and Methods for Measuring Implicit Learning. In E. Kennedy & J. Qian (Eds.) Advancing Educational Research with Emerging Technology. IGI Global.
- Rowe, Rowe, E., Asbell-Clarke, J., & Baker, R. (2019, April). Game-based measures of implicit learning. Structured poster session organized by Y.J. Kim titled Game-Based Assessment: How Has the Field Matured over the Past 10 years? AERA Annual Meeting, Toronto.
- Rowe, E., Asbell-Clarke, J., Baker, R., Gasca, S., Bardar, E., & Scruggs, R. (2018, April). Labeling Implicit Computational Thinking in Pizza Pass Gameplay. Late-breaking work presented at the ACM SIGCHI Conference on Human Factors in Computing Systems (CHI 18), Montreal. https://doi.org/10.1145/3170427.3188541
- Rowe, E., Asbell-Clarke, J., Baker, R., Gasca, S., Bardar, E., & Scruggs, R. (2017, April). Labeling Implicit Computational Thinking in Pizza Pass Gameplay. Late-breaking work presented at the ACM SIGCHI Conference on Human Factors in Computing Systems (CHI 18), Montreal. https://doi.org/10.1145/3170427.3188541
- Shute, V. J., Sun, C., & Asbell-Clarke, J. (2017). Demystifying computational thinking. Educational Research Review, 22, 142-158.
- Rowe, E., Asbell-Clarke, J., Cunningham, K. & Gasca, S. (2017, October). Assessing implicit computational thinking in Zoombinis gameplay: Pizza Pass, Fleens, and Bubblewonder Abyss. Work-in-progress presented at the ACM SIGCHI Annual Symposium on Computer-Human Interaction in Play, Amsterdam.
- Rowe, E., Asbell-Clarke, J., Gasca, S., & Baker, R. (2017, October). Computational thinking in Zoombinis gameplay. Spotlight session at the 8th Digital Media & Learning Conference in Irvine, CA.
- Rowe, E., Asbell-Clarke, J., Gasca, S., & Cunningham, K. (2017, August). Assessing implicit computational thinking in Zoombinis gameplay. Poster presented at the International Conference on the Foundations of Digital Games in Hyannis, MA.
- Rowe, E., Asbell-Clarke, J., Gasca, S., & Baker, R. (2017, April). Computational Thinking in Zoombinis Gameplay. Poster presented at the Cyberlearning Conference in Arlington, VA.
Additional Resources
- Related CADRE Spotlights
- CIRCL Primers
References
Brown, A. L. (1992). Design experiments: Theoretical and methodological challenges in creating complex interventions in classroom settings. The Journal of the Learning Sciences, 2(2), 141-178.
Cobb, P., Confrey, J., DiSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9-13.
Collins, A. (1992). Towards a design science of education. In E. Scanlon & T. O'Shea (Eds.), New directions in educational technology (pp. 15-22). Berlin: Springer
Dhombres, J. (1993). Is one proof enough? Travels with a mathematician of the baroque period. Educational Studies in Mathematics, 24(4), 401-419.
Hadwin, A. F., Wozney, L., & Pontin, O. (2005). Scaffolding the appropriation of self-regulatory activity: A socio-cultural analysis of changes in teacher–student discourse about a graduate research portfolio. Instructional Science, 33(5–6), 413–450.
Gentner, D., Loewenstein, J., & Thompson, L. (2003). Learning and transfer: A general role for analogical encoding. Journal of Educational Psychology, 95(2), 393.
Goldstone, R. L., Day, S., & Son, J. Y. (2010). Comparison. In Towards a theory of thinking (pp. 103-121). Springer, Berlin, Heidelberg.
Guo, J. P., & Pang, M. F. (2011). Learning a mathematical concept from comparing examples: The importance of variation and prior knowledge. European Journal of Psychology of Education, 26(4), 495-525.
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students’ learning. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 371-404). Greenwich, CT: Information Age
House, P. A., & Coxford, A. F. (1995). Connecting Mathematics across the Curriculum.1995 Yearbook. National Council of Teachers of Mathematics. Reston, VA.
Janssen, J., Erkens, G., Kirschner, P. A., & Kanselaar, G. (2012). Task-related and social regulation during online collaborative learning. Metacognition and Learning, 7(1), 25–43.
Loewenstein, J., & Gentner, D. (2001). Spatial mapping in preschoolers: Close comparisons facilitate far mappings. Journal of Cognition and Development, 2(2), 189-219.
Kumpulainen, K., & Mutanen, M. (1999). The situated dynamics of peer group interaction: An introduction to an analytic framework. Learning and Instruction, 9(5), 449-473.
Kurtz, K. J., Miao, C. H., & Gentner, D. (2001). Learning by analogical bootstrapping. The Journal of the Learning Sciences, 10(4), 417-446.
Mercer, N. (2002). Words and minds: How we use language to think together. Routledge.
Mercer, N., Dawes, L., Wegerif, R., & Sams, C. (2004). Reasoning as a scientist: Ways of helping children to use language to learn science. British Educational Research Journal, 30(3), 359-377.
Mercer, N., Wegerif, R., & Dawes, L. (1999). Children's talk and the development of reasoning in the classroom. British Educational Research Journal, 25(1), 95-111.
Namy, L. L., & Gentner, D. (2002). Making a silk purse out of two sow's ears: Young children's use of comparison in category learning. Journal of Experimental Psychology: General, 131(1), 5.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
National Governors Association. (2010). Common core state standards. Washington, DC.
Oakes, L. M., & Ribar, R. J. (2005). A comparison of infants' categorization in paired and successive presentation familiarization tasks. Infancy, 7(1), 85-98.
Pólya, G. (1963). Induction and analogy in mathematics. Princeton University Press.
Polya, G. (1973). How to solve it 2nd. New Jersey: Princeton University.
Polya, G. (1963). Induction and analogy in mathematics. Princeton University Press.
Rittle-Johnson, B., & Star, J. R. (2007). Does comparing solution methods facilitate conceptual and procedural knowledge? An experimental study on learning to solve equations. Journal of Educational Psychology, 99(3), 561.
Rittle-Johnson, B., & Star, J. R. (2009). Compared with what? The effects of different comparisons on conceptual knowledge and procedural flexibility for equation solving. Journal of Educational Psychology, 101(3), 529.
Rittle-Johnson, B., Star, J. R., & Durkin, K. (2009). The importance of prior knowledge when comparing examples: Influences on conceptual and procedural knowledge of equation solving. Journal of Educational Psychology, 101(4), 836.
Schoenfeld, A. H. (1983). Beyond the purely cognitive: Belief systems, social cognitions, and metacognitions as driving forces in intellectual performance. Cognitive science, 7(4), 329-363.
Schoenfeld, A. H. (1988). When good teaching leads to bad results: The disasters of'well-taught'mathematics courses. Educational Psychologist, 23(2), 145-166.
Schoenfeld, A. H. (2006). Design experiments. Handbook of Complementary Methods in Education Research, 193-206.
Shaffer, D. W., Collier, W., & Ruis, A. R. (2016). A tutorial on epistemic network analysis: Analyzing the structure of connections in cognitive, social, and interaction data. Journal of Learning Analytics, 3(3), 9–45.
Shavelson, R. J., & Towne, L. (Eds.). (2002). Scientific research in education. Committee on Scientific Principles for Education Research. Washington, DC: National Research Council.
Star, J. R., & Rittle-Johnson, B. (2008). Flexibility in problem solving: The case of equation solving. Learning and Instruction, 18(6), 565-579.
Star, J. R., & Rittle-Johnson, B. (2009). It pays to compare: An experimental study on computational estimation. Journal of Experimental Child Psychology, 102(4), 408-426.
Vinner, S. (1989). The Avoidance of Visual Considerations in Calculus Students. Focus on Learning Problems in Mathematics, 11, 149-56.
Xin, Y. P., Wiles, B., & Lin, Y. Y. (2008). Teaching Conceptual Model—Based Word Problem Story Grammar to Enhance Mathematics Problem Solving. The Journal of Special Education, 42(3), 163-178.