What would happen if a student who had just solved 3 + 5 came across the problem 3 + -5, -3 + 5, or even -3 + -5? We are investigating how factors, such as the order in which students learn integer problems, influences their integer understanding and solution strategies.
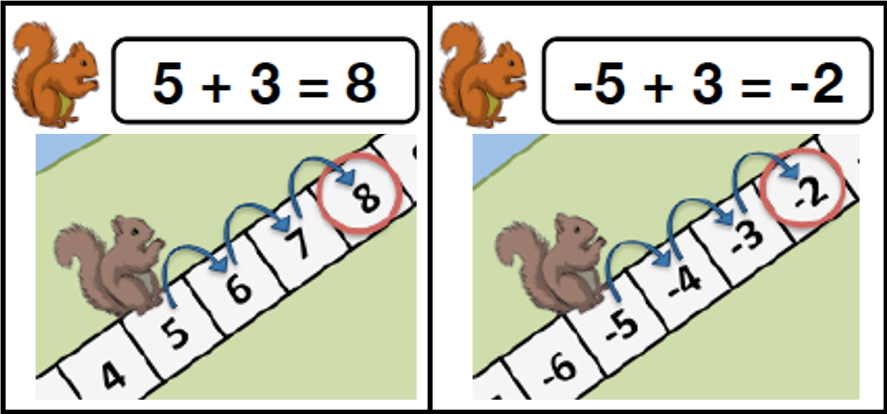
One challenge that students face when learning about integers and integer operations is building on and also modifying their prior understanding of whole numbers. Through our project we seek to clarify how students build upon and revise their whole number knowledge to learn and develop strategies with integers depending on the types of contrasting cases they experience. For example, students who first learn adding two negative integers in contrast with two positive ones (e.g., -3 + -5 vs. 3 + 5) may overlearn that problems with negative integers have negative answers. Therefore, they may be more likely to think that -3 + 5 is -8. On the other hand, students who first learn adding a positive integer to a negative integer (e.g., -3 + 5) may overlearn that they should always count up in the number sequence. Therefore, they may be more likely to think that -3 + -5 is 2. Through randomly assigning students to experimental conditions where they evaluate different contrasting cases of integer problems, we evaluate the role problem type sequence, with connections among language, operations, and symbols (e.g., + -2, plus negative two, and more negative two), plays in students’ learning of integer addition and subtraction.
One of the biggest challenges we’ve had in working with our data is the overwhelming realization of how complicated students’ learning of negative integers is. Students’ reasoning about integers involves their understanding of whole numbers’ quantities, number order, symbols, operations, and language—all of which take on new meaning with the introduction of negative integers. Students who may correctly answer a problem sometimes provide reasoning that indicates they do not have conceptual understanding of negative integers, leading us to change the way we determine if we should consider an answer correct or not.
- CADRE Project Page
- Book: Temperature Turmoil
Based on insights from this research, we wrote and illustrated a story illuminating the difficulty students have in thinking about magnitude versus number order and the use of language with integers, which is available in a digital form.